Estatística e visualização: analisando seus dados e obtendo resultados
Introdução
Sempre que você obtém um novo conjunto de dados para examinar, uma das primeiras tarefas que você precisa fazer é encontrar maneiras de resumir os dados de uma forma compacta e de fácil compreensão. É disso que se trata a estatística descritiva. Nesta aula vamos aprender funções de estatística descritiva usando R e fazer gráficos usando o pacote stat de gráficos básicos.
Para esta aula vamos usar o mesmo data frame da PNAD que olhamos nas aulas anteriores. Primeiro vamos importar os dados (você aprendeu como fazer isso na aula anterior, lembra?):
url <- "https://raw.githubusercontent.com/laddem/site/master/amostra_pnad.csv"
df <- read.csv(url)
head(df)
## Ano Trimestre UF V1022 V2007 V2009 V2010 VD2003
## 1 2021 1 Ceará Urbana Homem 80 Branca 2
## 2 2021 1 Distrito Federal Urbana Mulher 19 Parda 4
## 3 2021 1 Pernambuco Urbana Mulher 36 Preta 2
## 4 2021 1 Santa Catarina Urbana Homem 50 Parda 2
## 5 2021 1 São Paulo Urbana Mulher 43 Parda 3
## 6 2021 1 Goiás Urbana Homem 35 Parda 3
## VD3005 VD4016
## 1 16 anos ou mais de estudo NA
## 2 11 anos de estudo NA
## 3 12 anos de estudo 1045
## 4 5 anos de estudo 1500
## 5 9 anos de estudo 1600
## 6 14 anos de estudo 3000
Estatística descritiva em R
Com o objetivo de ter uma ideia sobre o que está acontecendo no data frame, precisamos calcular algumas estatísticas descritivas e desenhar alguns gráficos.
Somas
Para calcular a soma, a função mais usada é sum()
vetor<- c(1,3,2,5,6,10)
sum(vetor)
## [1] 27
sum(vetor[2:4])
## [1] 10
A função permite que você some um vetor específico, ou posições dentro deste vetor.
Exercício
Some as primeiras três posições da variável V2009 do data frame df
na.rm
Caso os dados tenham NA, será necessário usar o argumento na.rm = TRUE por que para o R a soma dos elementos será NA.
vetor <- c(2, 5, 10, 28, NA)
sum(vetor[3:5])
## [1] NA
sum(vetor[3:5], na.rm = TRUE)
## [1] 38
Exercício
Some as primeiras 30 observações da variável VD4016 do data frame df. O que aconteceu? Foi necessário usar na.rm?
Contagens
Podemos fazer contagens usando a função abaixo:
table(df$Trimestre)
##
## 1
## 1000
table(df$UF)
##
## Acre Alagoas Amapá Amazonas
## 19 52 12 35
## Bahia Ceará Distrito Federal Espírito Santo
## 52 53 14 39
## Goiás Maranhão Mato Grosso Mato Grosso do Sul
## 28 67 23 24
## Minas Gerais Pará Paraíba Paraná
## 104 36 21 40
## Pernambuco Piauí Rio de Janeiro Rio Grande do Norte
## 53 20 49 17
## Rio Grande do Sul Rondônia Roraima Santa Catarina
## 65 13 13 45
## São Paulo Sergipe Tocantins
## 82 10 14
table(df$V1022)
##
## Rural Urbana
## 257 743
table(df$V2010)
##
## Amarela Branca Indígena Parda Preta
## 7 407 3 506 77
A função table não serve apenas para contagens simples, mas também para tabulações cruzadas:
table(df$V1022, df$V2010)
##
## Amarela Branca Indígena Parda Preta
## Rural 0 83 1 160 13
## Urbana 7 324 2 346 64
table(df$V1022, df$V2007)
##
## Homem Mulher
## Rural 125 132
## Urbana 368 375
table(df$UF, df$V1022)
##
## Rural Urbana
## Acre 1 18
## Alagoas 26 26
## Amapá 0 12
## Amazonas 12 23
## Bahia 18 34
## Ceará 17 36
## Distrito Federal 1 13
## Espírito Santo 4 35
## Goiás 5 23
## Maranhão 27 40
## Mato Grosso 6 17
## Mato Grosso do Sul 5 19
## Minas Gerais 34 70
## Pará 15 21
## Paraíba 4 17
## Paraná 4 36
## Pernambuco 13 40
## Piauí 10 10
## Rio de Janeiro 1 48
## Rio Grande do Norte 3 14
## Rio Grande do Sul 16 49
## Rondônia 1 12
## Roraima 2 11
## Santa Catarina 8 37
## São Paulo 14 68
## Sergipe 3 7
## Tocantins 7 7
Essa forma de especificar é conhecida como forma “x,y”, mas há também outra forma especificar tabulações cruzadas, como um subconjunto de data.frame:
table(df[, c("UF", "V1022")])
## V1022
## UF Rural Urbana
## Acre 1 18
## Alagoas 26 26
## Amapá 0 12
## Amazonas 12 23
## Bahia 18 34
## Ceará 17 36
## Distrito Federal 1 13
## Espírito Santo 4 35
## Goiás 5 23
## Maranhão 27 40
## Mato Grosso 6 17
## Mato Grosso do Sul 5 19
## Minas Gerais 34 70
## Pará 15 21
## Paraíba 4 17
## Paraná 4 36
## Pernambuco 13 40
## Piauí 10 10
## Rio de Janeiro 1 48
## Rio Grande do Norte 3 14
## Rio Grande do Sul 16 49
## Rondônia 1 12
## Roraima 2 11
## Santa Catarina 8 37
## São Paulo 14 68
## Sergipe 3 7
## Tocantins 7 7
table(df[, c("V2007", "V2010")])
## V2010
## V2007 Amarela Branca Indígena Parda Preta
## Homem 5 201 2 247 38
## Mulher 2 206 1 259 39
table(df[, c("VD3005", "V2007")])
## V2007
## VD3005 Homem Mulher
## 1 ano de estudo 12 17
## 10 anos de estudo 8 16
## 11 anos de estudo 10 14
## 12 anos de estudo 105 111
## 13 anos de estudo 12 7
## 14 anos de estudo 6 13
## 15 anos de estudo 9 8
## 16 anos ou mais de estudo 51 61
## 2 anos de estudo 14 13
## 3 anos de estudo 16 15
## 4 anos de estudo 19 27
## 5 anos de estudo 44 46
## 6 anos de estudo 25 23
## 7 anos de estudo 13 20
## 8 anos de estudo 25 19
## 9 anos de estudo 44 27
## Sem instrução e menos de 1 ano de estudo 47 45
É possível fazer tabulações mais complexas, com 3 variáveis, mas eu deixo para vocês descobrirem por conta própria! Também explorem a função xtabs(), que faz algo parecido, mas com uma sintaxe diferente.
Médias
Entre as medidas de tendência central, temos a média, calculada no R pela função mean()
vetor<- c(20,10,30,4085,1292)
mean(vetor)
## [1] 1087.4
mean(vetor[2:4])
## [1] 1375
A função mean() também permite calcular a média especificando a posição das observações que você quer no cálculo.
Média “trimmed”
Quando nos deparamos com casos em os dados podem ser suspeitos, como este por exemplo: -15,2,3,4,5,6,7,8,9,12 o valor -15 é meio suspeito, porém não conseguimos saber se é verdadeiro ou não. A média é altamente sensível a um ou dois valores extremos e, portanto, não é considerado uma medida robusta. Uma forma de resolver é usando a média trimmed. Para calcular este tipo de média, o que acontece é que você descarta os valores mais extremos nas duas pontas do vetor (o maior e o menor) e depois tira a média de todo o resto.
Geralmente, descrevemos uma média trimmed em termos da porcentagem de observação de cada lado que é descartada. Por exemplo, uma média trimmed de 10% descarta os maiores 10% das observações e os menores 10% e, em seguida, toma a média dos 80% restantes das observações.
vetor<- c(-15,2,3,4,5,6,7,8,9,12)
mean(vetor)
## [1] 4.1
mean(vetor, trim = 0.1)
## [1] 5.5
Se eu pegar uma média trimmed de 10%, deixaremos os valores extremos de cada lado e pegaremos a média do resto como foi feita acima usando o argumento trim = 0.1
mean(df$VD4016, na.rm = T)
## [1] 2000.636
mean(df$VD4016, na.rm = T, trim = 0.05)
## [1] 1704.745
mean(df$VD4016, na.rm = T, trim = 0.1)
## [1] 1591.949
Exercício
Calcule a média da variável V2009 do data frame df. Calcule a média e média trimmed. Quais são as principais diferenças?
Medianas
A segunda medida de tendência central que se usa muito é a mediana. A mediana de um conjunto de observações é o valor que divide o conjunto de dados em duas partes iguais. A funcão do R que calcula a mediana é median()
vetor<- c(20,30, 50, 47,59)
median(vetor)
## [1] 47
Exercício
Calcule a mediana da variável V2009 do data frame df. Quais as diferenças encontradas em relação a média calculada no exercício anterior?
Amplitude
A amplitude é uma das medidas de dispersão calculada pelo R através da função range(). Além dela, podemos ver através do R, o valor máximo através da função max() e o valor mínimo através da função min() de um vetor de valores.
A amplitude basicamente calcula o valor máximo menos o valor mínimo de um vetor.
vetor<- c(20,30,60,80,17)
range(vetor)
## [1] 17 80
Podemos calcular esses valores também usando a função max() e min() separadamente
vetor<- c(20,30,60,80,17)
max(vetor)
## [1] 80
min(vetor)
## [1] 17
Exercício
Calcule o valor máximo, mínimo e a amplitude da variável V2009 do data frame df.
Percentis
A divisão dos conjunto de dados em percentuais é o que se denomina de percentil. Os percentis mais famosos são justamente o 1º quartil ( = percentil 25%), o 2º quartil ( = percentil 50% = mediana), e o 3º quartil (= percentil 75%). Para calcular o percentil no R, usa-se a função quantile() o argumento probs permite a especificação de outros percentis além do padrão.
quantile(df$V2009, probs = c(.25, .75))
## 25% 75%
## 18 55
quantile(df$V2009, probs = c(.1, .3, .5, .7, .9))
## 10% 30% 50% 70% 90%
## 7 22 36 49 67
Distância interquartil
A distância interquartil é uma medida de dispersão estatística, sendo igual à diferença entre o quartil superior (Q3) e quartil inferior (Q1). No R, a função que calcula o interquatil é IQR().
a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
IQR(a)
## [1] 0.85
Exercício
Calcule a distância interquatil da variável V2009 do data frame df da pnad. Que valor você encontrou? Compare com os valores encontrados no percentil 25% e 75%.
Variância
A variância de um conjunto de valores é calculada pelo R usando a função var().
b <- c(1, 2, 2.5, 4, 4.5, 5.5, 6, 6.4, 7, 7.5, 8)
var(b)
## [1] 5.492727
Exercício
Calcule a variância da variável V2009 do data frame df.
Desvio padrão
Pegue a raiz quadrada da variância e teremos mais uma medida conhecida como desvio padrão. Para calcular o desvio padrão no R, usamos a função sd() (Standard Deviation).
a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
sd(a)
## [1] 1.919043
Exercício
Calcule o desvio padrão da variável V2009 do data frame df.
Desvio absoluto da mediana
Cada observação no conjunto de dados fica a alguma distância do valor típico (a mediana). Portanto, o desvio absoluto da mediana(median absolute deviation - MAD) é uma tentativa de descrever a tendência de desvio um valor típico no conjunto de dados. A função que calcula essa medida pelo R chama-se mad(), para median absolute deviation.
a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
mad(a)
## [1] 0.59304
Exercício
Calcule o Desvio absoluto da mediana da variável V2009 do data frame df.
Sumário estatístico
Existe uma função do R que é capaz de calcular as principais medidas apresentadas acima, de uma vez, em uma única função. Dessa forma, é muito mais prático utilizar as funções que resumem algumas medidas estatísticas principais summary().
summary(df$V2009)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 18.00 36.00 36.94 55.00 104.00
summary(df$V2010)
## Length Class Mode
## 1000 character character
A função summary() se comporta de maneiras diferentes dependendo do tipo de variável, por exemplo, na variável V2009 numérica, a função summary() retorna as medidas: min, 1º quartil, mediana, média, 3º quartil e max. Na variável V2010, categórica, a função summary() retorna a frequência absoluta de cada categoria. É possível fazer o summary de um data frame inteiro de uma vez.
summary(df)
## Ano Trimestre UF V1022
## Min. :2021 Min. :1 Length:1000 Length:1000
## 1st Qu.:2021 1st Qu.:1 Class :character Class :character
## Median :2021 Median :1 Mode :character Mode :character
## Mean :2021 Mean :1
## 3rd Qu.:2021 3rd Qu.:1
## Max. :2021 Max. :1
##
## V2007 V2009 V2010 VD2003
## Length:1000 Min. : 0.00 Length:1000 Min. : 1.000
## Class :character 1st Qu.: 18.00 Class :character 1st Qu.: 2.000
## Mode :character Median : 36.00 Mode :character Median : 3.000
## Mean : 36.94 Mean : 3.609
## 3rd Qu.: 55.00 3rd Qu.: 4.000
## Max. :104.00 Max. :11.000
##
## VD3005 VD4016
## Length:1000 Min. : 50
## Class :character 1st Qu.: 1000
## Mode :character Median : 1262
## Mean : 2001
## 3rd Qu.: 2300
## Max. :19000
## NA's :613
Esse é um excelente exemplo do R utilizar a classe de um objeto para mudar o comportamento de uma função: summary() lê o atributo classe de cada vetor ou objeto que você passar como argumento e define um método adequado para resumir esse objeto.
Estatísticas por grupo
É muito comum que você precise olhar para estatísticas descritivas, divididas por alguma variável de agrupamento
Isso é muito fácil de fazer no R e há duas funções em particular que vale a pena conhecer: by() e aggregate().
A função by() mostra algo semelhante a função summary() porém dividido por grupo especificado no argumento INDICES.
by(data=df, INDICES=df$V1022, FUN=summary)
## df$V1022: Rural
## Ano Trimestre UF V1022
## Min. :2021 Min. :1 Length:257 Length:257
## 1st Qu.:2021 1st Qu.:1 Class :character Class :character
## Median :2021 Median :1 Mode :character Mode :character
## Mean :2021 Mean :1
## 3rd Qu.:2021 3rd Qu.:1
## Max. :2021 Max. :1
##
## V2007 V2009 V2010 VD2003
## Length:257 Min. : 0.00 Length:257 Min. : 1.000
## Class :character 1st Qu.: 18.00 Class :character 1st Qu.: 2.000
## Mode :character Median : 35.00 Mode :character Median : 3.000
## Mean : 37.01 Mean : 3.763
## 3rd Qu.: 54.00 3rd Qu.: 5.000
## Max. :104.00 Max. :11.000
##
## VD3005 VD4016
## Length:257 Min. : 50
## Class :character 1st Qu.: 500
## Mode :character Median :1022
## Mean :1199
## 3rd Qu.:1500
## Max. :5800
## NA's :169
## ------------------------------------------------------------
## df$V1022: Urbana
## Ano Trimestre UF V1022
## Min. :2021 Min. :1 Length:743 Length:743
## 1st Qu.:2021 1st Qu.:1 Class :character Class :character
## Median :2021 Median :1 Mode :character Mode :character
## Mean :2021 Mean :1
## 3rd Qu.:2021 3rd Qu.:1
## Max. :2021 Max. :1
##
## V2007 V2009 V2010 VD2003
## Length:743 Min. : 0.00 Length:743 Min. : 1.000
## Class :character 1st Qu.:18.00 Class :character 1st Qu.: 2.000
## Mode :character Median :37.00 Mode :character Median : 3.000
## Mean :36.92 Mean : 3.556
## 3rd Qu.:55.00 3rd Qu.: 4.000
## Max. :96.00 Max. :10.000
##
## VD3005 VD4016
## Length:743 Min. : 50
## Class :character 1st Qu.: 1100
## Mode :character Median : 1500
## Mean : 2237
## 3rd Qu.: 2700
## Max. :19000
## NA's :444
Neste exemplo, a função by mostra as medidas separadas pelas categorias de variáveis V1022, ou seja, mostra o summary para categoria Urbana e um summary para categoria Rural.
Para a aggregate() também é necessário especificar três argumentos. O lado esquerdo da fórmula é usado para indicar qual variável você deseja analisar e o lado direito, quais variáveis são usadas para especificar os grupos.
aggregate(formula = V2009 ~ V1022 + V2007, data = df, FUN = mean)
## V1022 V2007 V2009
## 1 Rural Homem 35.60800
## 2 Urbana Homem 36.13859
## 3 Rural Mulher 38.33333
## 4 Urbana Mulher 37.67733
Escores e testes
O R inclui toda uma suíte de funções para trabalhar com distribuições estatísticas, elas seguem uma convenção de nomes que indicam <função_estatística><tipo_de_distribuição>, exemplo:
No caso da distribuição de poisson, são quatro funções, uma para a densidade:
dpois(0:7, lambda = 1)
## [1] 3.678794e-01 3.678794e-01 1.839397e-01 6.131324e-02 1.532831e-02
## [6] 3.065662e-03 5.109437e-04 7.299195e-05
Uma para a distribuição:
ppois(0:7, lambda = 1)
## [1] 0.3678794 0.7357589 0.9196986 0.9810118 0.9963402 0.9994058 0.9999168
## [8] 0.9999898
Uma para os quartis (ou quantis):
qpois(c(.3, .5, .9, .95, .99), lambda = 1)
## [1] 0 1 2 3 4
Uma para gerar distribuições aleatórias:
rpois(100, lambda = 1)
## [1] 0 1 0 0 1 1 0 2 0 1 1 3 2 0 0 1 1 1 1 1 0 1 1 1 1 0 0 1 1 2 0 2 1 1 0 1 1
## [38] 1 1 1 2 1 1 0 3 2 2 2 1 0 0 1 1 1 1 1 1 1 1 0 0 1 3 1 1 2 2 0 0 2 0 1 1 1
## [75] 0 2 0 1 1 1 0 0 0 1 0 2 1 2 0 2 0 1 1 1 1 1 1 0 1 0
O mesmo ocorre com as outras distribuições estatísticas, por exemplo, a distribuição normal terá as funções:
?dnorm
?pnorm
?qnorm
?rnorm
E a distribuição binomial:
?dnorm
?pnorm
?qnorm
?rnorm
E assim sucessivamente.
Uma última coisa, você pode usar esses funções para calcular um p valor a partir de uma estatística escore de um teste:
x <- 1:10
y <- 11:20
t <- (mean(x) - mean(y)) / sqrt(var(x) / length(x) + var(y) / length(y))
pt(t, df = 18)
## [1] 3.751569e-07
Onde x e y são duas variáveis, t é o valor da estatística t calculada pela fórmula e pt() é a função de distribuição da distribuição T de Student. Lógico que, sendo um teste extremamente comum, ele já foi programado em uma função no R:
t.test(x, y)
##
## Welch Two Sample t-test
##
## data: x and y
## t = -7.3855, df = 18, p-value = 7.503e-07
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -12.844662 -7.155338
## sample estimates:
## mean of x mean of y
## 5.5 15.5
Exercício
Utilize seus conhecimentos de indexação e distribuições para fazer verificar se as diferenças de renda entre a população rural e urbana são estatisticamente significativas ao nível de 0.05.
Correlações
Em geral, um dos últimos assuntos cobertos numa introdução a estatística, as correlações também são implementadas em R. Aqui, veremos a aplicação da função cor para pares de variáveis e para um data frame como um todo.
Abaixo, vocês encontram um exemplo da medição da correlação entre duas variáaveis:
cor(df$VD2003, df$V2009)
## [1] -0.3656368
E um teste de correlação linear de Pearson:
cor.test(df$VD2003, df$V2009)
##
## Pearson's product-moment correlation
##
## data: df$VD2003 and df$V2009
## t = -12.41, df = 998, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4181517 -0.3106861
## sample estimates:
## cor
## -0.3656368
Abaixo, podemos ver que a função cor() tem uma saída diferente se usada em um data frame, para tornar isso possível, é preciso primeiro selecionar apenas as variáveis numéricas:
cor(df[, c("V2009", "VD2003", "VD4016")])
## V2009 VD2003 VD4016
## V2009 1.0000000 -0.3656368 NA
## VD2003 -0.3656368 1.0000000 NA
## VD4016 NA NA 1
Exercício
Faça um teste de correlação linear entre a idade (V2009) e o número de moradores (VD2003). O que esse resultado significa?
use=???
Nosso resultado é a matriz de correlações entre as variáveis de df! Porém, temos um problema, os NAs presentes na variável VD4016 se propagaram para todas as correlações envolvendo-a. Quando executamos operações com vetores, aprendemos que na.rm era a solução para esse tipo de situação. Mas na.rm é uma solução para problemas envolvendo apenas uma variável. O que fazer com os NAs que podem estar vindo de múltiplas variáveis diferentes?
- Poderíamos optar por remover todos os
NAs de todas as variáveis envolvidas e computar apenas as correlações entre valores válidos, mas sacrificaríamos grande parte da nossa amostra.
cor(df[, c("V2009", "VD2003", "VD4016")], use = "complete.obs")
## V2009 VD2003 VD4016
## V2009 1.0000000 -0.2271063 0.1655302
## VD2003 -0.2271063 1.0000000 -0.1032641
## VD4016 0.1655302 -0.1032641 1.0000000
- Poderíamos remover apenas os valores inválidos dos pares que estão sendo correlacionados, preservando o máximo de amostra possível.
cor(df[, c("V2009", "VD2003", "VD4016")], use = "pairwise.complete.obs")
## V2009 VD2003 VD4016
## V2009 1.0000000 -0.3656368 0.1655302
## VD2003 -0.3656368 1.0000000 -0.1032641
## VD4016 0.1655302 -0.1032641 1.0000000
Existem outras opções na ajuda da função ?cor, mas além do padrão que é "everything", o mais comum é utilizar essas duas. No caso que estamos considerando, não há diferença entre os resultados porque a única variável com NA é VD4016, mas em situações em que duas ou mais variáveis contenham NAs é provável que os resultados de "complete.obs" e "pairwise.complete.obs" sejam diferentes.
Exercício
Agora calcule correlações lineares entre as variáveis renda (VD4016), idade (V2009) e número de moradores (VD4016) tratando adequadamente os NAs na variável renda.
Visualizações
Desenhar gráficos ajuda a compreender os dados. Para isso, é importante desenhar “gráficos exploratórios” que o ajudem a aprender sobre os dados à medida que os analisa. Iremos mostrar os principais tipos de gráficos que usamos para analisar e apresentar os dados e, mostrar como criar esses gráficos no R.
Você pode pensar em um gráfico como uma pintura. Você começa com uma tela vazia. Cada vez que você usa uma função gráfica, ela pinta algumas coisas novas em sua tela. Mais tarde, você pode pintar mais coisas por cima, se quiser; mas, assim como na pintura, você não pode “desfazer” seus traços. Se você cometer um erro, terá que jogar fora sua pintura e começar de novo. Felizmente, isso é muito mais fácil de fazer ao usar o R do que ao pintar um quadro na vida real: você deleta o gráfico e começa novos comandos para fazer um novo gráfico.
No RStudio, o gráfico será exibido em um device e neste caso irá aparecer na área plot, no canto superior direito (uma aba do lado da sessão Environment que já vimos nas aulas anteriores). É possível também salvar o gráfico como um arquivo de imagem jpeg, png, pdf, postscript, tiff, bmp, entre outros formatos.
Diferentes sistemas gráficos no R
Existem diferentes pacotes para desenhar gráficos no R, pois existem diferentes formas computacionais de desenhar gráficos, ou seja, diferentes sistemas de gráficos. Um sistema gráfico define uma coleção de comandos gráficos de baixo nível sobre o que desenhar e onde desenhar. Algo que surpreende a maioria dos novos usuários é a descoberta de que realmente existem sistemas gráficos totalmente independentes, gráficos tradicionais conhecidos (no pacote graphics) e gráficos de grade (no pacote grid). Esses dois sistemas diferentes são praticamente incompatíveis um com o outro.
O R tem vários pacotes diferentes, cada um fornece um conjunto de comandos gráficos de alto nível. Um único comando de alto nível é capaz de desenhar um gráfico inteiro, completo com uma variedade de opções de personalização. A maioria dos comandos (mas não todos) do pacote graphics é de alto nível, e neste sentido, funciona para o sistema dos gráficos tradicionais. Todos esses comandos tendem a compartilhar um estilo visual comum, embora haja alguns gráficos que diferem um pouco no estilo.
Do outro lado do sistema de gráficos, o universo do sistema de grade depende fortemente de dois pacotes diferentes –lattice e ggplot2– os dois fornecem um estilo visual bastante diferente. Como você provavelmente já deve ter adivinhado, há um monte de funções separadas que você precisa aprender se quiser usar gráficos do pacote lattice ou fazer uso do ggplot2.
Para esta aula vamos falar sobre as ferramentas gráficas básicas do sistema tradicional do pacote graphics.
Parâmetros gráficos vs argumentos de função
As diferentes funções de plotagem do graphics compartilham de alguns argumentos gerais que podem ser usados na maioria das funções e outros argumentos que são próprios de cada função de plotagem. Existem diferentes parâmetros que podem ser usados.
O que exatamente é um parâmetro no gráfico? Basicamente, a ideia é que existem algumas características de um gráfico que são bastante universais: por exemplo, independentemente do tipo de gráfico que você está desenhando, você provavelmente precisa especificar a cor a ser usada no gráfico, certo? Então é muito provável que haja algum tipo de argumento para cada função gráfica no R? Bem, mais ou menos. A fim de evitar centenas de argumentos para cada função, o que o R faz é referir-se a um monte desses “parâmetros gráficos” que têm um propósito bem geral. Os parâmetros gráficos podem ser alterados diretamente usando a função low-level par().
?par
Se você procurar saber mais, vai perceber que existem milhares de argumentos que podem ser especificados usando a função par(). Raramente você vai precisar usar a função par() diretamente, você pode colocar os argumentos diretamente na função que você está usando para construir algum gráfico.
Plot
Introdução ao scatterplot através de um exemplo de plotagem simples
Antes de mostrar os tipos de funções gráficas mais específicas, vamos começar com a função básica plot().
fibonacci <- c(1,1,2,3,5,8,13)
plot(fibonacci)
Como você pode ver, o R plotou os valores armazenados no vetor fibonacci no eixo vertical (eixo y) e o índice correspondente no eixo horizontal (eixo x). Ou seja, no eixo x, o valor seria o da posição dentro do vetor fibonacci, e no eixo y, o valor que está naquela posição. O importante a se notar ao usar a função plot(), é que é um outro exemplo de uma função genérica muito parecida com a função summary() que aprendemos na aula anterior.
A função plot() depende de dois argumentos, x (a primeira entrada, que é necessária) e y (que é opcional). Isso o torna (a) extremamente poderoso quando você pega o jeito e (b) imprevisível, quando você não tem certeza do que está fazendo.
Tipo de gráfico
Você pode personalizar a aparência do gráfico atual! Para começar, vamos dar uma olhada nas opções mais importantes que a função plot() fornece para você usar (lembrando que estamos lidando com uma função genérica, neste caso a função plot.default(), já que é aquela que faz todo o trabalho), que é o argumento type. O argumento type especifica o estilo visual do do gráfico. Os valores possíveis para o argumento type: “p”, “l”, “h”, “o”, “b”, “s”, “S”, “c”, “n”
plot(fibonacci, type = "p")
plot(fibonacci, type = "l")
plot(fibonacci, type = "h")
plot(fibonacci, type = "o")
plot(fibonacci, type = "b")
plot(fibonacci, type = "s")
plot(fibonacci, type = "S")
plot(fibonacci, type = "c")
plot(fibonacci, type = "n")
Como você pode ver, alterando o argumento type, você pode obter uma aparência diferente para seu gráfico. Em outras palavras, no que diz respeito ao R, a única diferença entre um gráfico de dispersão e um gráfico de linha é que para desenhar um gráfico de dispersão você coloca type = "p", e no de linha type = "l" como se fossem equivalentes, porém estilos diferentes. Mas, um gráfico de linha implica que há alguma noção de continuidade de um ponto para o próximo, enquanto um gráfico de dispersão não.
- type = “p” desenha somente pontos
- type = “o” desenha uma linha sobre os pontos
- type = “h” desenha barras verticais
- type = “s” desenha as linhas em formato de escada, indo do horizontal para o vertical
- type = “S” desenha as linhas em formato de escada, indo do vertical para o horizontal
- type = “l” desenha somente a linha, sem os pontos.
- type = “c” desenha somente as linhas conectando os pontos, sem passar por cima deles
- type = “n” não desenha nada (aparentemente isso de alguma forma pode ser útil?)
Exercício
Plote um gráfico, usando a função plot(), da variável V2009 do data frame df. O que ocorre se você tenta plotar a variável Trimeste como gráfico de dispersão? E de linha?
Agora vamos para tipos de gráficos mais específicos. Iremos começar pelos histogramas.
Histogramas
Os histogramas são uma das formas mais simples e úteis de visualizar dados e você consegue ter uma impressão geral dos seus dados.
O que um histograma faz? Ele divide os valores possíveis em caixas e, em seguida, conta o número de observações que caem dentro de cada bin.
A função do R base que cria um histograma é hist(). Dentro desta função existem alguns argumentos especificos dentre eles o argumento breaks que define o número de quebras ou bins que o seu histograma terá
hist(df$V2009)
A maneira como você especifica as quebras tem um grande efeito na aparência do histograma, por isso é importante ter certeza de escolher as quebras de maneira sensata.
hist(vetor, breaks = 3)
hist(vetor, breaks = 20)
Em geral, o R faz um bom trabalho ao selecionar as quebras por conta própria, uma vez que faz uso de alguns truques que os estatísticos desenvolveram para selecionar automaticamente as caixas certas para um histograma, mas, no entanto, geralmente é uma boa ideia brincar com as quebras um pouco para ver o que acontece.
É possível usar outros argumentos dentro da função hist(). Iremos listar todos os argumentos que podem ser usados no final desta aula.
Exercício
Considere a variável VD4016 do data frame df. Desenho o histograma, e use diferentes valores no argumento breaks, teste aquele que ficará melhor para esta variável. O que acontece se você tentar fazer um histograma da variável V2010?
Boxplots
Uma outra alternativa, em relação ao histograma, são os BoxPlots. Lembra das informações que a função summary() nos dá?
Vamos relembrá-la aqui.
summary(df$V2009)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 18.00 36.00 36.94 55.00 104.00
O boxplot nada mais é do que uma maneira visual de ver essas informações (min, max, 1º quartil, mediana, média, 3º quartil) contidas no summary().
A função que desenha um boxplot, adivinha? Chama-se boxplot(). Como sempre, há muitos argumentos opcionais que você pode especificar se quiser, mas na maioria das vezes você pode apenas deixar o R escolher por padrão. Dito isso, vou substituir um dos padrões para começar especificando a opção de intervalo (argumento range), mas na maioria das vezes você não vai querer fazer isso (explicarei o porquê em um minuto). Vamos tentar o seguinte comando:
boxplot(df$V2009, range = 100)
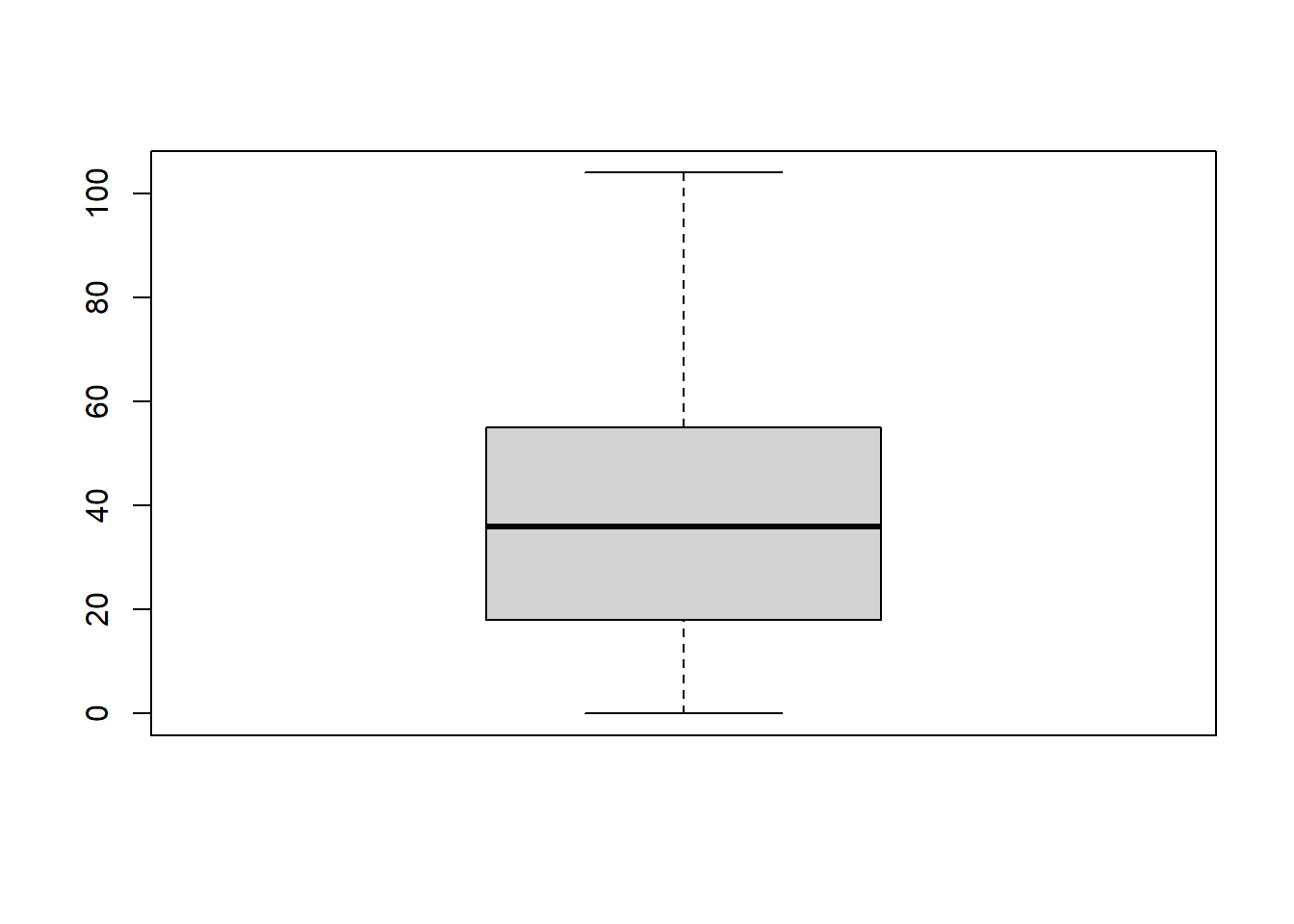
Quando você olha para este gráfico, é assim que você deve interpretá-lo: a linha grossa no meio da caixa é a mediana; a caixa em si abrange a faixa do 25º ao 75º percentil; e os “traços” cobrem toda a faixa do valor mínimo ao valor máximo.
Na prática, não é bem assim que boxplots geralmente funcionam. Na maioria das aplicações, os “traços” (whiskers) não cobrem todo o intervalo do mínimo ao máximo. Em vez disso, eles vão para o ponto de dados mais extremo que não excede um certo limite. Por padrão, esse valor é 1,5 vezes o intervalo interquartil, correspondendo a um valor de 1,5. Qualquer observação cujo valor esteja fora desse intervalo (range) é representada graficamente como um círculo em vez de ser coberta pelos traços e é comumente referida como outlier.
boxplot(df$V2009)
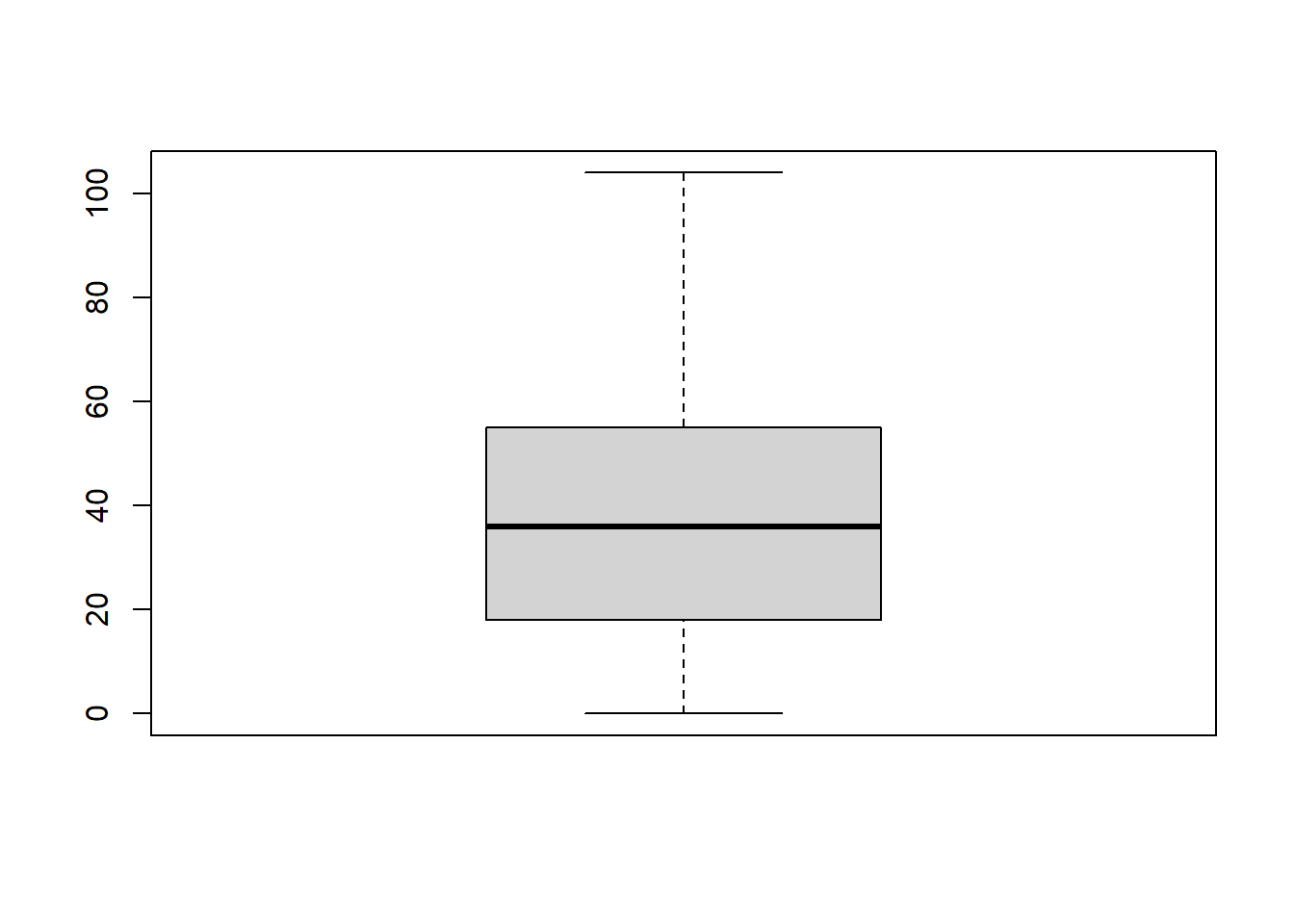
Exercício
Faça um boxplot da variável VD4016. O que você vê de diferente em relação a variável V2009 usada no exemplo anterior? Como você interpretaria esse boxplot.
É possível usar dentro da função boxplot(), o argumento formula que irá relacionar duas variáveis. Veja:
boxplot(formula = V2009 ~ V2010,
data = df)
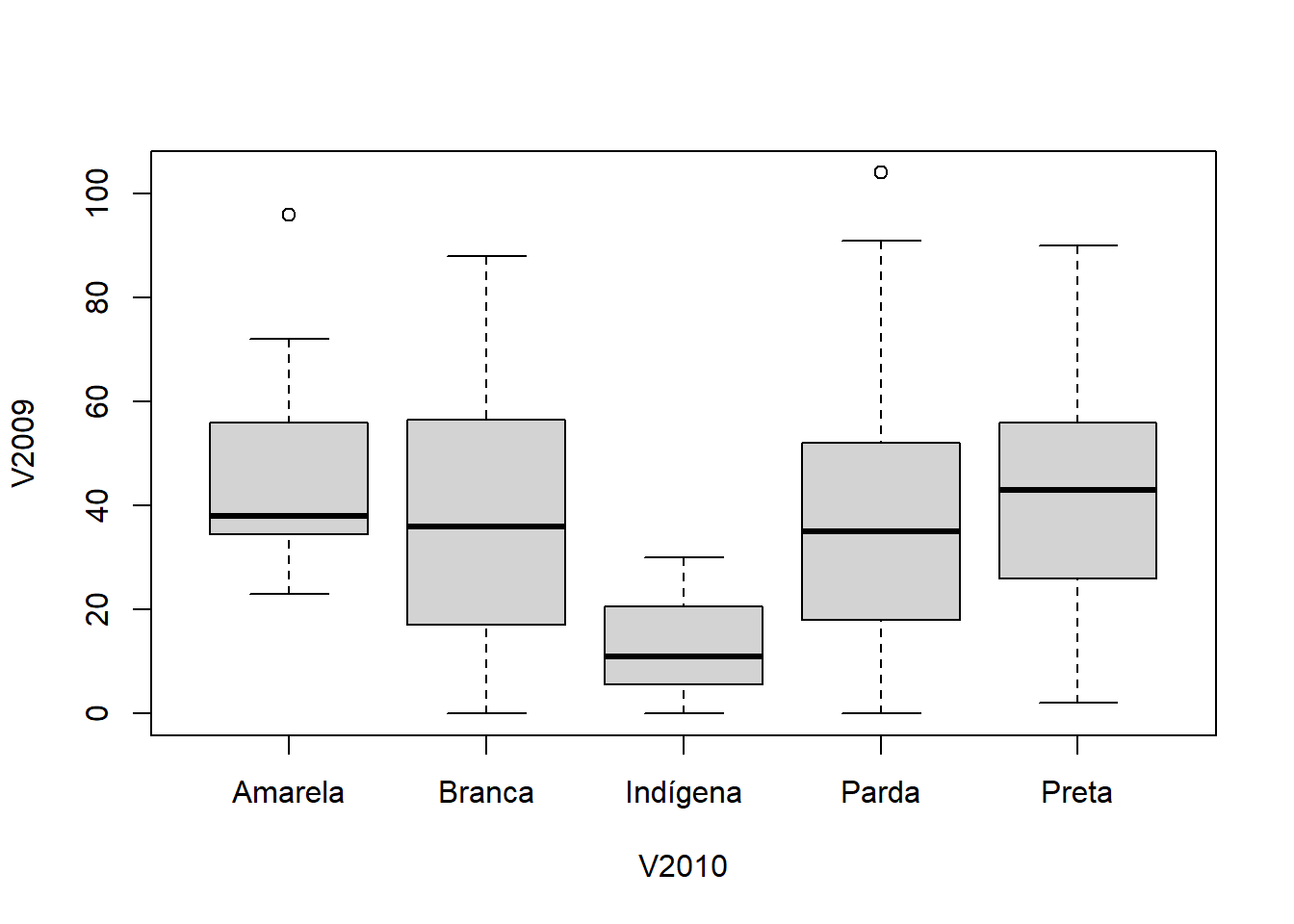
Diagramas de dispersão
A gente já viu um pouquinho do que é um gráfico de dispersão quando usamos a função plot() no começo desta seção de visualização de gráficos. Lembra?
Mas agora, vamos mostrar como fazer um gráfico de dispersão (scatterplot) relacionando duas variáveis, e não plotando somente uma como foi feito no exemplo lá no começo.
Nesse tipo de gráfico, cada observação corresponde a um ponto: a localização horizontal do ponto representa o valor da observação em uma variável e a localização vertical exibe seu valor na outra variável. Em muitas situações, você realmente não tem uma opinião clara sobre quais as relações causais entre as duas variáveis escolhidas, então tanto faz qual você ira colocar no eixo x e qual você irá colocar no eixo y.
No entanto, em muitas situações, você tem uma ideia bastante clara de qual variável você acha que é mais provável de ser causal, ou pelo menos tem algumas suspeitas nessa direção. Nesse caso, então é convencional plotar a variável de causa no eixo x, e a variável de efeito no eixo y.
plot(x= df$V2009,
y = df$VD4016)
É possível escrever as variáveis através do argumento formula e especificando o data frame no argumento separado data
plot(V2009 ~ VD4016,
data = df)
Adicionar linhas a um scatterplot
Caso você queira adicionar uma linha no gráfico de dispersão é necessário definir pelos argumentos x e y, a localização da linha e da coluna dentro da função lines()
plot(V2009 ~ VD4016,
data = df)
lines(x = c(40,15000),
y = c(40,45),
lwd = 2)
Matriz de scatterplots
Freqüentemente, você deseja examinar as relações entre várias variáveis ao mesmo tempo. Uma ferramenta útil para fazer isso é produzir uma matriz de scatterplots, análoga à matriz de correlação. A matriz de scatterplots é possível usando a função pairs() .
pairs(df[c("VD4016", "V2009", "VD2003")])

Uma maneira alternativa de chamar a função pairs(), que pode ser útil em algumas situações, é especificar as variáveis a serem incluídas usando uma fórmula unilateral. Por exemplo:
pairs(formula = ~ VD4016 + V2009 + VD2003,
data = df)

Barras
Outra forma de gráfico que você pode desejar fazer é o gráfico de barras. A principal função que você pode usar no R para desenhá-los é a função barplot()
# Primeiro, é preciso transformar em fator
f <- as.factor(df$VD3005)
# Agora sim, podemos tabular e plotar
escolaridade <- tabulate(f)
barplot(escolaridade)
labels_esc<-levels(f)
barplot(height = escolaridade, names.arg = labels_esc)
O problema ao executar este gráfico, é que os nomes das categorias são grandes demais e não couberam no gráfico, não aparecendo todos, para isso, existe o argumento las, que rotaciona os rótulos (labels).
head(df)
## Ano Trimestre UF V1022 V2007 V2009 V2010 VD2003
## 1 2021 1 Ceará Urbana Homem 80 Branca 2
## 2 2021 1 Distrito Federal Urbana Mulher 19 Parda 4
## 3 2021 1 Pernambuco Urbana Mulher 36 Preta 2
## 4 2021 1 Santa Catarina Urbana Homem 50 Parda 2
## 5 2021 1 São Paulo Urbana Mulher 43 Parda 3
## 6 2021 1 Goiás Urbana Homem 35 Parda 3
## VD3005 VD4016
## 1 16 anos ou mais de estudo NA
## 2 11 anos de estudo NA
## 3 12 anos de estudo 1045
## 4 5 anos de estudo 1500
## 5 9 anos de estudo 1600
## 6 14 anos de estudo 3000
barplot(height = escolaridade, names.arg = labels_esc, las = 2)
Exercício
Crie um barplot para a variável V2007 do dataframe df.
O primo pobre: gráficos de pizza
Para calcular um gráfico de pizzas, a função se chama pie()
f <- as.factor(df$V2007)
sexo <- tabulate(f)
labels_sexo <- levels(f)
pie(sexo, labels = labels_sexo)
Exercício
Crie um gráfico de pizza da variável V1022.
Parâmetros globais
É possível usar alguns parâmetros globais a partir da função par(). Vamos especificar alguns aqui.
Caso você queira mudar as margens do gráfico, podemos usar o parâmetro mar. Parece simples, mas em alguns situações acaba sendo mais complicado do que você pode imaginar. Em princípio, o tamanho das margens é estruturado através do parâmetro gráfico chamado mar, então tudo o que precisamos fazer é alterar esse parâmetro. Primeiro, vamos ver o que o argumento especifica. O argumento é um vetor contendo quatro números: especificando a quantidade de espaço na parte inferior, na esquerda, na parte superior e, em seguida, na direita. As unidades são “número de linhas”.
par(mar = c( 10.1, 4.1, 4.1, 2.1))
Não há saída visível aqui, mas nos bastidores o R mudou os parâmetros gráficos associados ao dispositivo atual (lembre-se, na terminologia todos os gráficos são desenhados em um “dispositivo” ou device). Agora que isso foi feito, poderíamos usar exatamente o mesmo comando para plotar um gráfico, mas desta vez você veria que todos os rótulos se ajustam, porque o R agora vai deixar o dobro de espaço para os rótulos na parte inferior. No entanto, como agora descobri como fazer com que os rótulos sejam exibidos corretamente, posso também brincar com algumas das outras opções, todas as quais você já viu antes:
f <- as.factor(df$VD3005)
escolaridade <- tabulate(f)
barplot(escolaridade)
labels <-levels(f)
barplot(height = escolaridade,
names.arg = labels,
las = 2)
O argumento mfrow permite que você combine mais de um gráfico em uma mesma “página”. É um vetor c(num de linhas,num de colunas).
par(mfrow=c(1,2))
pie(sexo, labels = labels_sexo)
barplot(height = escolaridade,
names.arg = labels_esc,
las = 2)
Salvando seus gráficos
Usando a interface do RStudio
Se você estiver executando o R através do Rstudio, a maneira mais fácil de salvar sua imagem é clicar no botão “Export” no painel Plot (ou seja, a área do Rstudio onde todos os gráficos aparecem). Veremos um menu que contém as opções “Salvar plotagem como PDF” e “Salvar plotagem como imagem”. Qualquer uma das versões funciona. Ambos abrirão caixas de diálogo que fornecem algumas opções para salvar seu gráfico em forma de imagem.
Usando grDevices
A função dev.list() lista todos os dispositivos gráficos que existem no dispositivo nesse momento
boxplot(df$V2009)
dev.list()
## png
## 2
O que isso significa é que há um dispositivo gráfico (dispositivo 2) que está aberto no momento e é uma janela com uma figura.
O R entende que seus dispositivos gráficos podem estar rodando simultâneamente. O dispositivo da janela Plots do RStudio se chama RStudioGD, no windows, o dispositivo se chama windows, em outros sistemas operacionais, os nomes são diferentes, mas a ideia é a mesma. Para ver os dispositivos abertos, use:
dev.list()
## png
## 2
Em geral, faz sentido escolher o que você quer de fato plotar e depois salvar isso num arquivo. Mas se você quiser salvar todos os dispositivos ativos no momento, use:
dev.print( device = jpeg,
filename = "thisfile.jpg",
width = 480,
height = 300)
## png
## 2
Essa função guardará todos os seus dispositivos abertos num arquivo jpeg chamado thisfile.jpg, com largura 480 pixels e largura 300 pixels e em seguida, fechará os gráficos. Na prática, o mais comum é fazer o salvamento de forma mais consciente, primeiro, fechando todos os dispositivos abertos (pela vassourinha ou usando a função abaixo):
dev.off()
## null device
## 1
Depois, você plota o gráfico que deseja salvar:
par(mfrow=c(1,2))
pie(sexo, labels = labels_sexo)
barplot(height = escolaridade,
names.arg = labels_esc,
las = 2)
E só então chama dev.print()
dev.print(device = jpeg,
filename = "thisfile.jpg",
width = 480,
height = 300)
## png
## 2
A parte filename = “thisfile.jpg” diz ao R como nomear o arquivo gráfico, e os argumentos width = 480 (largura) e height = 300 (altura) dizem ao R para desenhar uma imagem com 300 pixels de altura e 480 pixels de largura. Se você quiser um tipo diferente de arquivo, apenas altere o argumento do dispositivo de jpeg para outro. O salva em png, tiff e bmp que funcionam exatamente da mesma maneira que o comando jpeg, mas produzem diferentes tipos de arquivos.
Execute o processo de listar todos os dispostivos abertos, fechá-los, plotar um gráfico de sua preferência e então salvá-lo num arquivo usando as funções dev.___.
Customização de gráficos
Títulos de gráficos e eixos
Uma das primeiras coisas que você vai querer fazer ao personalizar seu gráfico é usar alguns labels diferentes. Você pode querer especificar rótulos de eixo mais apropriados, adicionar um título ou adicionar um subtítulo. Os argumentos que você precisa especificar para que isso aconteça são:
• main: Uma sequência de caracteres contendo o título.
• sub: Uma string de caracteres contendo o subtítulo.
• xlab: Uma string de caracteres contendo o rótulo do eixo x.
• ylab: Uma string de caracteres contendo o rótulo do eixo y.
Exemplo geral de como usar esses argumentos:
fibonacci <- c( 1,1,2,3,5,8,13 )
plot(x = fibonacci,
main = "Título do Gráfico",
sub = "subtítulo do gráfico",
xlab = "título do eixo x",
ylab = "título do eixo y")
Customização de fonte
Há alguns recursos interessantes para os quais vale a pena conhecer. Em primeiro lugar, observe que o subtítulo está desenhado abaixo do gráfico, como conseqüência, quase nunca uso legendas. Você pode ter uma opinião diferente, é claro, mas o importante é que você se lembre onde a legenda realmente vai.
Em segundo lugar, observe que o R coloca texto em negrito e um tamanho de fonte maior para o título. É possível alterar essas configurações. O título, pelos padrões do R, são muito grandes e chamam muita atenção.
Para esse fim, há um monte de parâmetros gráficos que você pode usar para personalizar o estilo da fonte:
• font.main: estilo da fonte usado para o título do gráfico
• font.sub: o subtítulo
• font.axis: os número perto das marcas nos eixos
• font.lab: os rótulos dos eixos
Esses argumentos são números em vez de nomes: valor 1 corresponde a texto simples, 2 significa negrito, 3 significa itálico e 4 significa negrito itálico.
- Cores
-
col.main,col.sub,col.axis,col.lab: Esses parâmetros fazem praticamente o que o nome diz: cada um especifica uma cor em parte de um texto, seja do título (main), do subtítulo (sub), título dos eixos (lab) ou os número das marcas dos eixos (axis).O R tem uma grande lista de nomes para cores, digite
colours()para ver uma lista de 650 nomes de cores que ele reconhece. - Tamanho
-
cex.main,cex.sub,cex.axis: A parte “cex” aqui é abreviação de “expansão de caracteres” e é essencialmente um valor de ampliação. Por padrão, todos eles são definidos com um valor de 1, exceto para o título da fonte:cex.mainque possue uma ampliação padrão de 1.2, a fonte do título é 20% maior do que as outras por padrão do R. - Família
-
family: esse argumento especifica a família da fonte para usar: a maneira mais simples de usar é definir como “sans”, “serif” ou “mono”, correspondendo a uma fonte san serif, uma fonte serif ou uma fonte monospaced Se desejar, você pode fornecer o nome de uma fonte específica, mas tenha em mente que diferentes sistemas operacionais usam fontes diferentes, então provavelmente é mais seguro não mudar esse argumento. Mas caso queira tentar, esse é o argumento necessário.
fibonacci <- c( 1,1,2,3,5,8,13 )
plot(x = fibonacci,
main = "Título do Gráfico",
xlab = "título do eixo x",
ylab = "título do eixo y",
font.main = 1,
family = 'serif',
cex.main = 1,
font.axis = 2,
col.lab = "gray50",
col.axis = 'blue')
Cores
col: este argumento muda a cor do gráfico através de um string com o nome dela, assim como mostrado no argumento para mudar a cor da fonte dos títulos, esse é o jeito mais simples.
Forma
pch: O parâmetro de caractere gráfico é um número, geralmente entre 1 e 25. O que ele faz é definir o símbolo que será usado para desenhar os pontos que ele plota.
Tamanho
cex: Este parâmetro descreve um fator de expansão de caractere (ou seja, ampliação) para os caracteres traçados. Por padrão o cex = 1, mas se você quiser símbolos maiores em seu gráfico, você deve especificar um valor maior que 1.
Tipo de linha
lty: define o tipo de linha que o R irá desenhar. Tem sete valores que você pode especificar usando um número entre 0 e 7, ou usando uma seqüência de caracteres: “blank”, “solid”, “dashed”, “dotted”, “dotdash”, “longdash”, “twodash”.
Espessura de linha
lwd: este argumento muda a espessura da linha desenhada no gráfico. O valor padrão é 1. Neste sentido, valores maiores produzem linhas mais grossas e valores menores produzem linhas mais finas.
fibonacci <- c( 1,1,2,3,5,8,13 )
plot(x = fibonacci,
type = "b",
col = "blue",
pch = 19,
cex = 5,
lty = 2,
lwd = 4)
Eixos
Escalas dos eixos
Caso você queira é possível mudar a escala dos eixos. O R faz um bom trabalho em escolar os limites inferiores e superiores dos eixos, mas as vezes é necessário mudar os limites. Os argumentos necessários para fazer essas alterações são xlim para o eixo x e ylim para o eixo y. O argumento aceita um vetor de duas posições, uma com o limite inferior e outra com o superios c(0,40).
Remover títulos
O argumento ann é um argumento que aceita TRUE ou FALSE e serve para você excluir algum título que você não queira que apareça no gráfico caso coloque ann = FALSE, o título especificado não irá aparecer.
Remover eixos
axes: esse também é um argumento lógico como o argumento anterior. Suponha que você não queira que o R desenhe os eixos. Para suprimir os eixos, tudo que você precisa fazer é adicionar o argumento axes = FALSE. Isso removerá os eixos e a numeração, mas não os rótulos dos eixos (ou seja, o texto ylab e xlab).
Manter área de plotagem
Suponha que você tenha removido os eixos definindo axes = FALSE, mas ainda deseja ter uma caixa simples desenhada ao redor do gráfico; ou seja, você só queria se livrar da numeração e das marcas de seleção, mas deseja manter a área. Para fazer isso, você define frame.plot = TRUE.
plot( x = fibonacci,
xlim = c(0, 15),
ylim = c(0, 15),
ann = FALSE,
axes = FALSE,
frame.plot = TRUE)

Argumentos específicos de cada função
-
Função
hist()e alguns argumentos. -
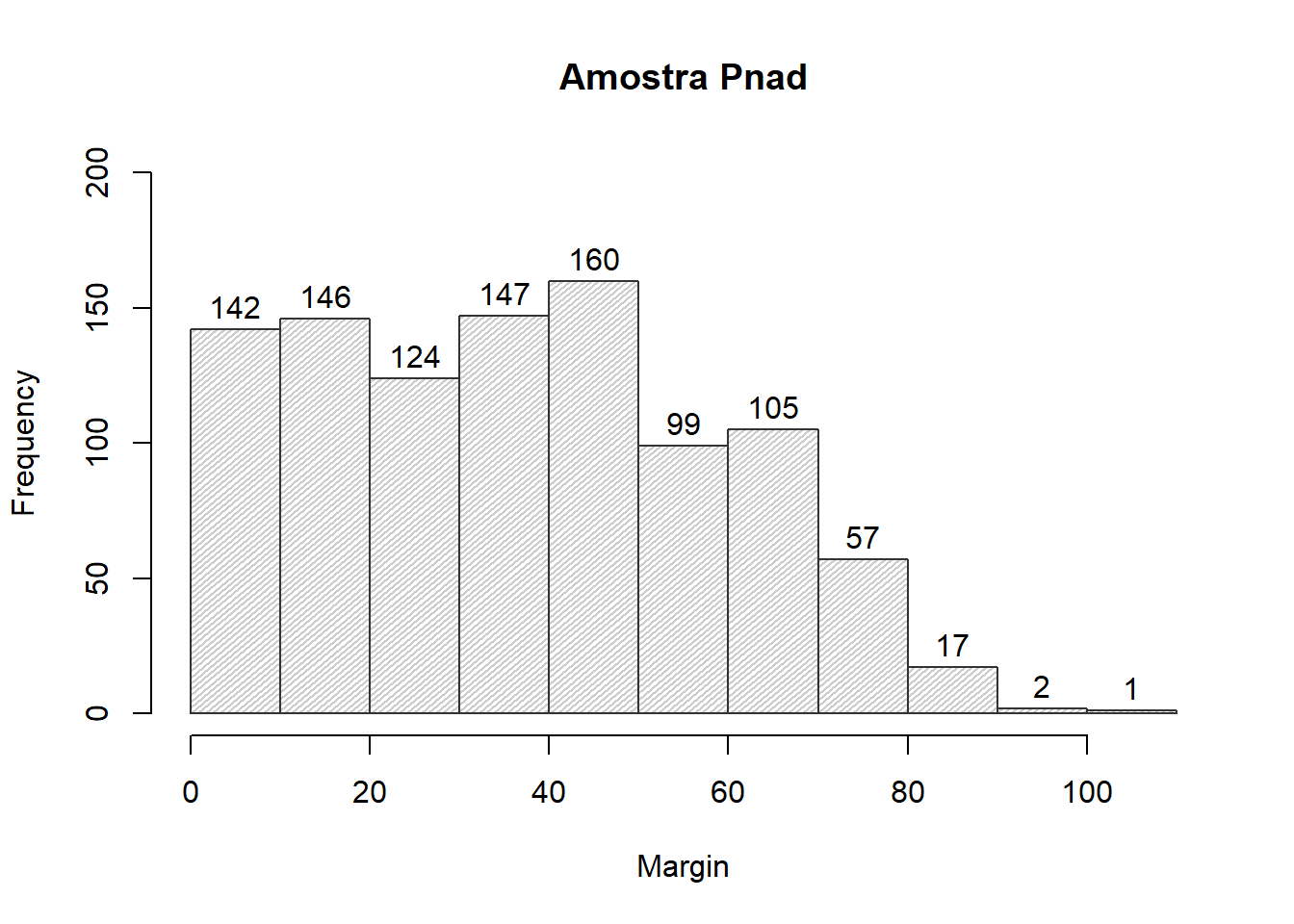
Linhas de sombreamento: argumentos
densityeangleesses argumentos adicionam linhas diagonais para sombrear as barras: o valor no argumentodensityé um número que indica quantas linhas por polegada deve ser desenhada (o valor padrão de NULL significa sem linhas) e oangleé um número que indica a quantos graus a partir da horizontal as linhas devem ser traçadas (padrão angle = 45 graus). -
Especificidades quanto às cores:
col,border. Você também pode alterar as cores: neste caso, o parâmetro colore a cor do sombreamento (ou as linhas de sombreamento, se houver, ou a cor do interior das barras, se não houver), e o argumento deborderdefine a cor das bordas das barras -
labels. Você também pode anexar rótulos a cada uma das barras usando o argumentolabels. A maneira mais simples de fazer isso é definirlabels= TRUE, caso em que o R adicionará um número logo acima de cada barra, sendo esse número o número exato de observações dentro daquele bin. Como alternativa, você mesmo pode escolher os labels, inserindo um vetor de strings, por exemplo, labels = c (“rótulo 1”, “rótulo2”, “etc”)
hist(x = df$V2009,
main = "Amostra Pnad",
xlab = "Margin",
density = 40,
angle = 40,
border = "gray20",
col = "gray80",
labels = TRUE,
ylim = c(0,200)
)
Além da gama usual de parâmetros gráficos que você pode ajustar para fazer o gráfico parecer bonito, você também mudar qualquer outros elementos que fazem parte de um boxplot.
Com o argumento border é possível mudar a cor dos os elementos gráficos do boxplot, exceto a barra central que representa a mediana (borda), de modo a chamar mais atenção para a mediana do que para o resto do boxplot.
As partes do boxplot que você pode personalizar são:
- box. A caixa que cobre o intervalo interquartil.
- med. A linha usada para mostrar a mediana.
- whisk As linhas verticais usadas para desenhar os traços inferiores e superiores.
- staple As barras transversais nas extremidades os traços inferiores e superiores.
- out. Os pontos usados para mostrar os outliers.
As seguintes especificações dos gráficos são necessárias para mudar algumas das partes do boxplot listadas acima:
-
Para aumentar a largura/espessura:
boxwex,staplewex,outwex. Esses são fatores de escala que governam a largura de várias partes do gráfico. O fator de escala padrão é (geralmente) 0.8 para a caixa e 0.5 para as outras duas partes. -
Para mudar o tipo de linha:
boxlty,medlty,whisklty,staplelty,outlty. Os valores para esses argumentos são iguais aos usados no parâmetro regularlty, com duas exceções. Há uma opção adicional onde você pode definirmedlty = "blank"para suprimir a linha mediana completamente (útil se você quiser desenhar um ponto para a linha mediana em vez de plotar). Da mesma forma, por padrão, o tipo de linha outlier é definido comooutlty = "blank", porque o comportamento padrão é desenhar outliers como pontos em vez de linhas. -
Para mudar a Largura da linha:
boxlwd,medlwd,whisklwd,staplelwd,outlwd. Eles alteram as larguras de linha para os elementos relevantes e se comportam da mesma maneira que o parâmetro regularlwd. A única coisa a notar é que o valor padrão para omedlwdé três vezes o valor dos outros. -
Para mudar a cor das linhas dos principais elementos:
boxcol,medcol,whiskcol,staplecol,outcol. Especifique uma cor da mesma maneira que você faz normalmente em outros argumentos de alteração de cores já mostrados por aqui. -
Cor de preenchimento da caixa do boxplot:
boxfill -
para mudar o formato do ponto:
medpch,outpch. Eles se comportam como o parâmetro regularpch. -
tamanho dos pontos:
medcex,outcex. Parâmetros de tamanho para os pontos usados para plotar medianas e outliers. Eles só são significativos se os pontos correspondentes forem realmente plotados. Portanto, para o boxplot padrão, que inclui pontos atípicos, mas usa uma linha em vez de um ponto para desenhar a mediana, apenas o parâmetrooutcexé significativo. -
Cores de fundo:
medbg,outbg. Novamente, as cores de fundo só são significativas se os pontos forem realmente traçados.
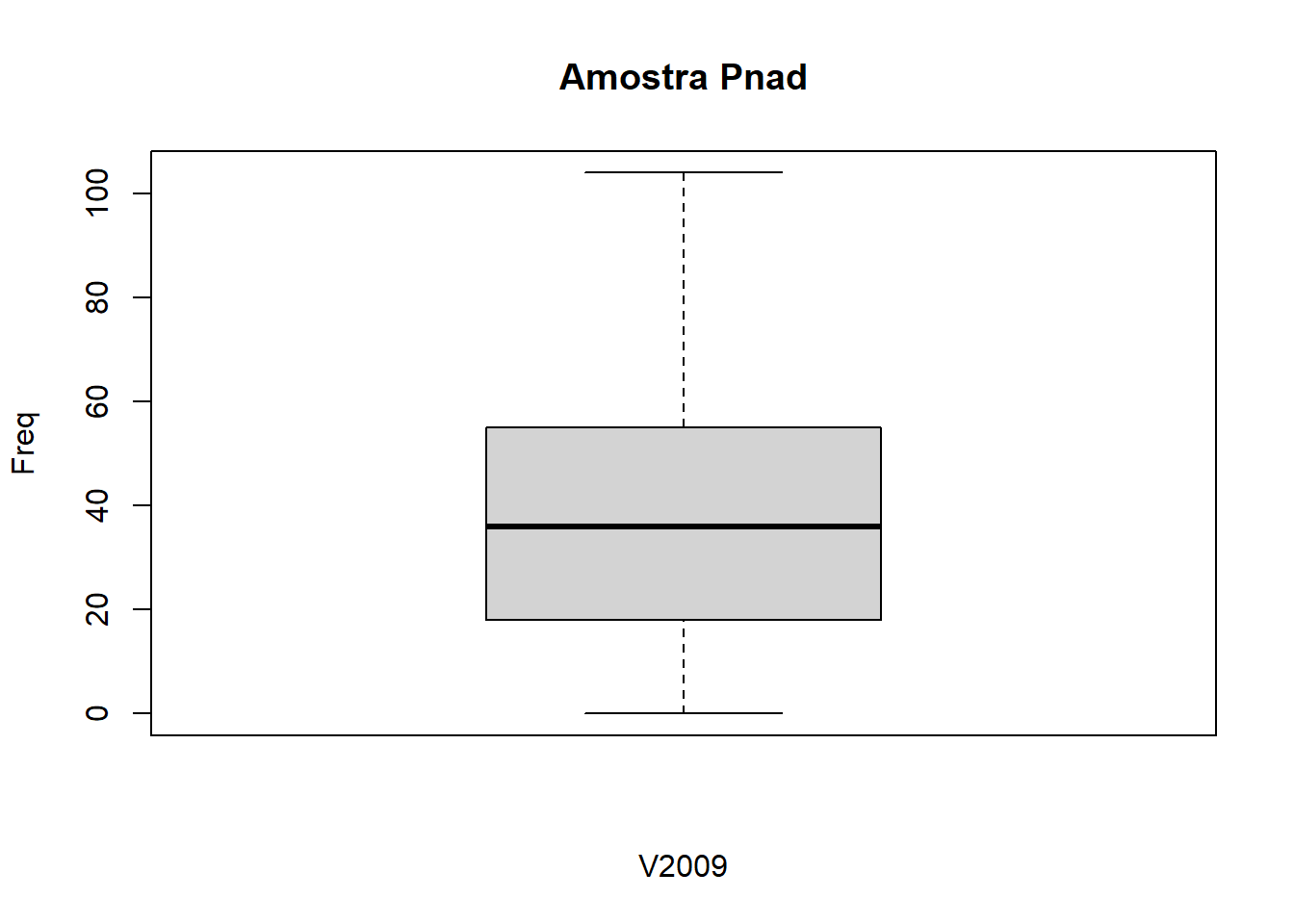
boxplot(x = df$V2009,
main = "Amostra Pnad",
xlab = "V2009",
ylab = "Freq")
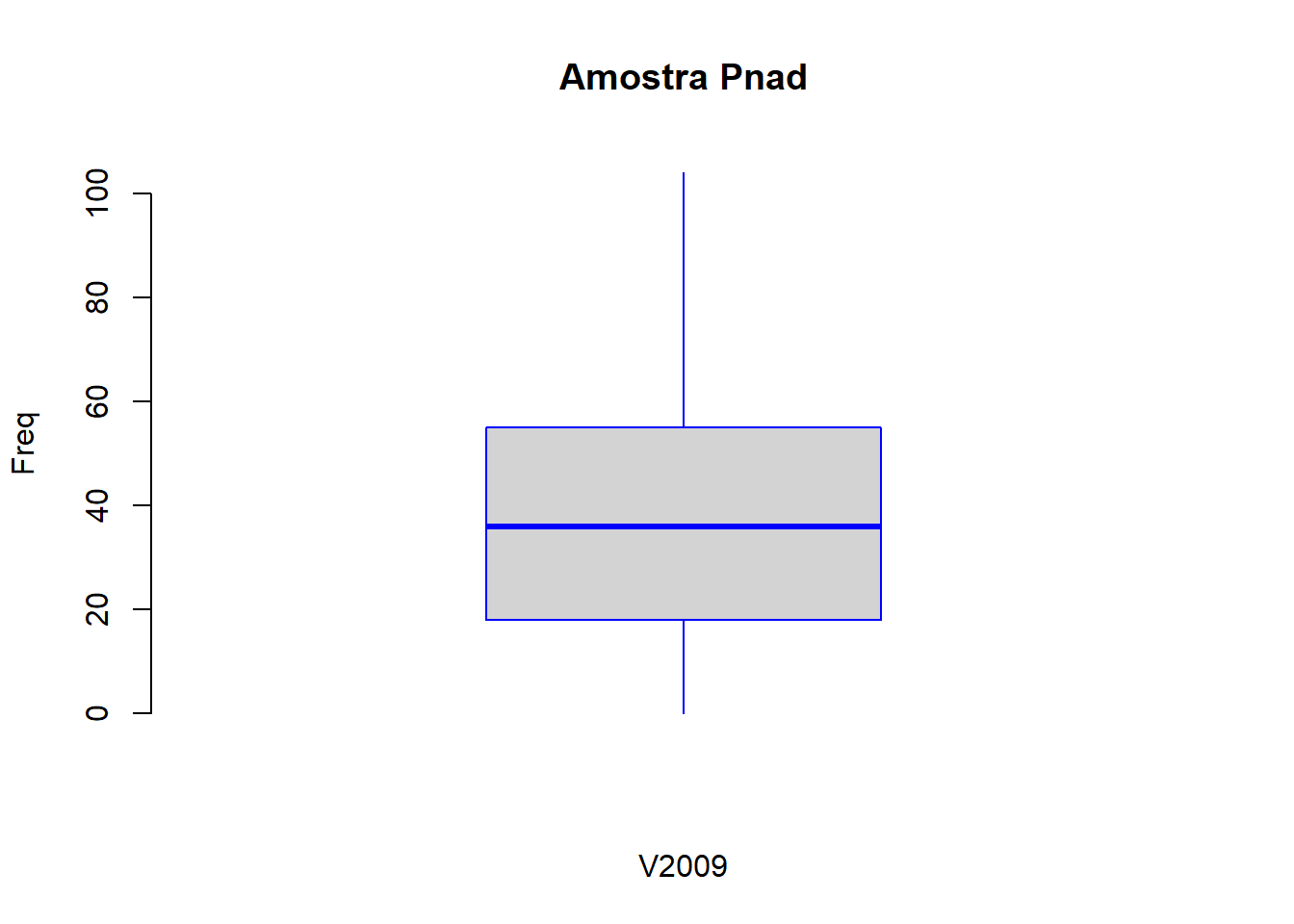
boxplot(x = df$V2009,
main = "Amostra Pnad",
xlab = "V2009",
ylab = "Freq",
border = "blue",
frame.plot = FALSE,
staplewex = 0,
whisklty = 1)
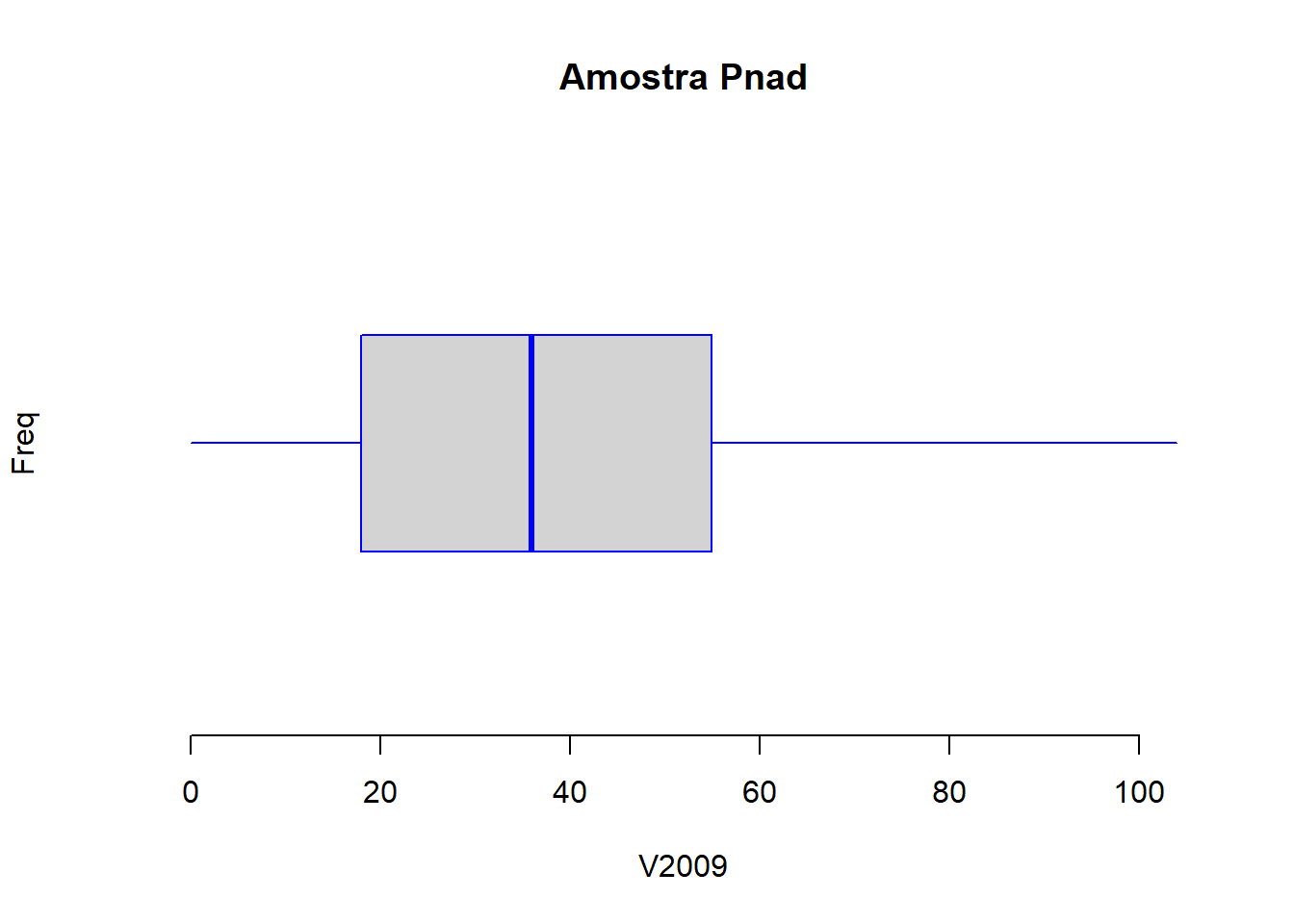
Se você quiser que o boxplot apareça horizontalmente, coloque o argumento horizontal = TRUE:
boxplot(x = df$V2009,
main = "Amostra Pnad",
xlab = "V2009",
ylab = "Freq",
border = "blue",
frame.plot = FALSE,
staplewex = 0,
whisklty = 1,
horizontal = TRUE)
Revisão
Nesta aula vimos algumas funções principais que calculam medidas usadas em estatística descritiva que permitem você entender melhor os seus dados e o que eles podem estar querendo mostrar para você:
- entre as funções que nos retornam uma medida única, aprendemos:
sum(),mean(),median(),range(),max(),min(),quantile(),IQR(),var(),sd()emad(). - a função
table()permite que você faça a contagem de observações em uma determinada categoria, assim como permite cruzar a contagem em duas variáveis. - as funções que entregam várias medidas sumarisadas:
summary(),by(),aggregate() - vimos também a função
cor()e as funções de testes estatísticos:
Além disso, vimos diferentes formas de fazermos gráficos básicos com a função global plot() e também aprendemos as funções para gráficos específicos como hist() (para histogramas), barplot() (para gráficos de barras), pie() para gráficos de pizza e boxplot() (bom, o nome é auto explicativo)
Exercícios
- Usando as funções de medidas individuais, rode o dataset ‘airquality’ (se você escrever assim no R, ele já mostra o dataset).
head(airquality)
## Ozone Solar.R Wind Temp Month Day
## 1 41 190 7.4 67 5 1
## 2 36 118 8.0 72 5 2
## 3 12 149 12.6 74 5 3
## 4 18 313 11.5 62 5 4
## 5 NA NA 14.3 56 5 5
## 6 28 NA 14.9 66 5 6
-
Crie um histograma para a variável airquality$Temp.
-
Use a função que sumarisa as principais informações de estatística básica e também construa um boxplot para comparar as informações escritas e visuais para as seguintes variáveis do dado airquality: Wind, Temp and Ozone).
# Exemplo
summary(airquality$Wind)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.700 7.400 9.700 9.958 11.500 20.700
- Agora usando somente os dados da amostra da pnad que temos visto até agora, faça uma análise descritiva usando as medidas individiuais, as de correlação e as de contagem. Além disso observe as diferenças entre a medida sumary para uma variável numérica e uma variável categórica.
head(df)
## Ano Trimestre UF V1022 V2007 V2009 V2010 VD2003
## 1 2021 1 Ceará Urbana Homem 80 Branca 2
## 2 2021 1 Distrito Federal Urbana Mulher 19 Parda 4
## 3 2021 1 Pernambuco Urbana Mulher 36 Preta 2
## 4 2021 1 Santa Catarina Urbana Homem 50 Parda 2
## 5 2021 1 São Paulo Urbana Mulher 43 Parda 3
## 6 2021 1 Goiás Urbana Homem 35 Parda 3
## VD3005 VD4016
## 1 16 anos ou mais de estudo NA
## 2 11 anos de estudo NA
## 3 12 anos de estudo 1045
## 4 5 anos de estudo 1500
## 5 9 anos de estudo 1600
## 6 14 anos de estudo 3000
Algumas ideias:
a. Use a função table para ver as relações entre a variável V1022 e V2007. Faça também para a variável V2007 e V2010. Veja as contagens de observações para cada categoria e entenda um pouco melhor o perfil dos dados.
b. Faça as medida resumo para a ver a média, mediana, quartis da sua amostra.
- Depois de fazer as análises descritivas, faça gráficos para ver os dados de forma visual, com o mesmo dado da pnad usado no exercício 4.
Ideias:
a. Faça um histograma das variáveis numéricas, talvez um boxplot também seja interessante. b. Faça um gráfico de barras para as variáveis categóricas.