Programando: scripts, controle de fluxo e iteração

Programas

Até esse momento, olhamos para as diferentes possibilidades de uso do R para analisar informações de maneira relativamente desestruturada. Vimos na primeira aula a forma como o R armazena informações em objetos e trabalha com eles através de funções. Na segunda aula, aprendemos a recuperar essas informações e fazer alterações nesses objetos através da indexação dos objetos, seja diretamente, indicando o índice onde a informação se encontra, seja indiretamente, através de testes lógicos.

Na terceira aula, vimos muitas funções pré-programadas que nos ajudam a descrever os dados através de conceitos de estatística, como medidas de tendência central e dispersão, bem como uma forma de visualizar essas medidas através de gráficos simples.

Hoje, gostaria de levar a atenção de vocês de volta a um ponto curto da aula 1: a estruturação de todas essas operações para produzir alguma coisa concreta. Seus programas provavelmente não serão pedaços soltos de importação de dados, ou uma coleção de objetos e funções, em geral, eles tem um objetivo claro e seguem uma sequência lógica, como produzir um grupo de tabelas sobre variáveis de interesse, ou vários gráficos que você pode utilizar em publicações ou em relatórios. E é disso que se trata construir um programa.

Estrutura de um programa

Em primeiro lugar, é útil estabelecer uma distinção: uma coisa é o programa e outra é a sua implementação em uma linguagem de programação. O programa não está limitado às tarefas que conhecemos ou que o software é capaz de realizar, ele descreve o que desejamos fazer e os passos necessários para atingir esse objetivo. Pode ser necessário realizar passos do programa fora do R, isso não importa. O mais importante é que o seu programa seja possível e que seus passos sigam uma sequência lógica bem fundamentada.

Um bom exemplo dessa distinção é que muitas vezes o nosso primeiro passo, obter dados, é executado usando nosso navegador ou nossos pés para ir até fontes de dados e trazê-las para o nosso computador.

Em muitos casos, por conveniência, podemos fazer alterações nessas fontes de dados através de um outro software, com o qual estamos familiarizados, antes de trazer para o R. Da mesma forma, no final de um processo de análise no R, podemos levar os resultados para outros programas onde vamos produzir os produtos finais, como textos, relatórios, postagens, publicaçóes, ou mesmo outras linguagens de programação como o Python. Assim, o nosso programa não se confunde com aquilo que de fato implementaremos no R.

Tarefas em série

Em geral, programas são compostos de uma série de tarefas que são executadas em ordem. Por exemplo:

• Vou até o site do open.datasus e baixo os dados sobre a vacinação em São Paulo
• Importo os dados no R
• Faço o tratamento da qualidade das informações, dos valores nulos, etc
• Construo tabelas de frequências de vacinação por grupo etário
• Transformo as tabelas de frequências em proporções do total
• Produzo um gráfico de barras estilo “pirâmide etária”
• Exporto as tabelas e gráficos para um editor de texto no qual produzo um relatório

A implementação dessas tarefas em série no R é muito simples: o R lê suas rotinas de cima para baixo, assim, basta que o encadeamento das operações respeite essa ordem para que seu programa funcione.

Tarefas em paralelo

Apesar da aparente simplicidade, muitas tarefas envolvem esquemas mais complexos:

• Algumas operações devem ser executadas apenas em alguns casos
• Algumas operações devem ser repetidas muitas vezes

Por exemplo, no meu programa de análise da vacinação, eu preciso transformar minhas tabelas de frequência em proporções do total. Mas total de que? Total da população em geral? Total da população por sexo? Total por grupo etário? Eu posso imaginar uma situação em que, para os municípios com menos de 50.000 habitantes, calcule o total por sexo, e para os municípios com mais de 50.000 habitantes, calcule o total geral.

Independente de se o exemplo faz sentido, o que é importante vocês levarem é que é necessário criar uma bifurcação no meu programa:

• Se a população > 50.000, uma operação deve ser realizada
• Se a população < 50.000, outra operação deve ser realizada

Em todas as linguagens de programação, essas operações são implementadas através de estruturas lógicas de se -> então; senão -> então, ou, if -> then; else -> then.

O outro problema que precisamos resolver frequentemente, é a repetição de uma operação. Por exemplo:

• Preciso contar o número de vacinados para cada grupo etário
• Preciso calcular as proporções para cada grupo etário

Mesmo que implicitamente, estamos tratando da repetição de uma operação muitas e muitas vezes. Em programação, isso é chamado de “loop”, ou laço.

Exemplo de um programa:

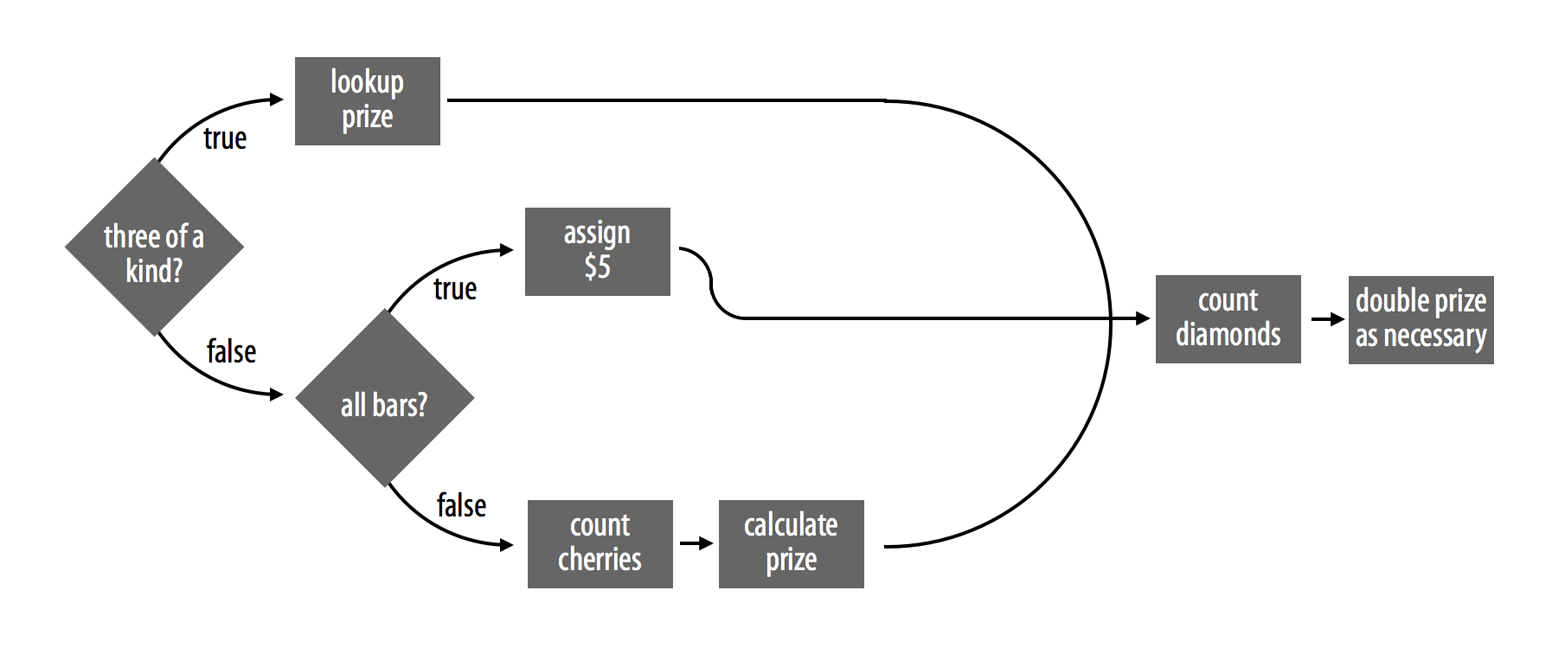
Estratégia de programação

Ok, mas você tem autonomia para construir seus programas da forma como você preferir, com um pouco de esforço e bateção de cabeça, dá pra fazer qualquer programa funcionar. Porque falar de estratégias então? Bom, se você aderir a algumas convenções você pode facilitar muito a sua vida, e evitar problemas comuns que ocorrem na hora que sentamos diante do computador para implementar nossos programas. Então, seguem algumas dicas:

Comece no papel

Antes de sentar no computador, descreva as atividades a serem realizadas em um papel. Eu costumo manter um bloco de notas do lado do computador para isso. Pode ser um bloco eletrônico, no próprio computador. O importante é que você tenha acesso a um documento que delineia o que você quer obter e o passo a passo para chegar lá que não depende do código que de fato será rodado pelo computador. Isso é extremamente útil porque programar é um trabalho cansativo e as vezes difícil, o que faz com a gente se perca e tenha aquele sentimento de “putz, o que eu estava fazendo mesmo?”.

Além disso, atualize seu programa a medida que você o implementa. Muitas vezes, nós estimamos mal a dificuldade de realizar uma tarefa. Em outros casos, várias tarefas podem ser feitas de uma só vez com facilidade. Procure atualizar seu programa original para refletir essas mudanças no nível de complexidade e no número de tarefas.

Divida o trabalho em tarefas menores

Ao desenhar um programa na nossa imaginação, não temos muita clareza da real dificuldade de realização de determinadas tarefas até que de fato nos sentamos para realizá-las. Quando isso ocorrer, não tente pular etapas: quebre suas tarefas em subtarefas menores até que elas possam ser realizadas com mais facilidade. Lembre-se que, ao contrário de um ser humano, o computador nunca se cansa de repetir pequenas tarefas milhões de vezes, então se utilize disso para simplificar ao máximo os passos sequenciais e paralelos necessários para realizar uma tarefa.

Crie exemplos mínimos para testar seu código

Se você está inseguro sobre a saída de uma função ou o resultado de um cálculo, crie um pequeno exemplo para testá-lo. Assim, você adquire controle e segurança sobre o input e o output (ou a entrada e a saída), bem como evita cometer erros de programação que são difíceis de identificar depois. Utilize seus conhecimentos de vetores e data frames para criar pequenos experimentos e verifique se o programa está executando-os corretamente. Lembre-se que uma das grandes vantagens de um computador é que se um código funciona para 10 casos, ele funciona para 10.000.000 de casos.

Criando programas no R

Tudo bem, estamos com nosso programa na mão e sentamos diante do computador. E agora?

Comece a implementar os passos em série no R, verificando que cada passo foi bem sucedido antes de ir para o próximo, evite pular etapas a menos que você já seja um programador experiente. É melhor ir dando cada passo e se certificando de que tudo está correndo bem. Vamos ver um exemplo de implementação de programa agora. Vou começar importando nossa mini-amostra da PNAD 2021, 1o trimestre.

url <- "https://raw.githubusercontent.com/laddem/site/master/amostra_pnad.csv"
df <- read.csv(url)
head(df)

##    Ano Trimestre               UF  V1022  V2007 V2009  V2010 VD2003
## 1 2021         1            Ceará Urbana  Homem    80 Branca      2
## 2 2021         1 Distrito Federal Urbana Mulher    19  Parda      4
## 3 2021         1       Pernambuco Urbana Mulher    36  Preta      2
## 4 2021         1   Santa Catarina Urbana  Homem    50  Parda      2
## 5 2021         1        São Paulo Urbana Mulher    43  Parda      3
## 6 2021         1            Goiás Urbana  Homem    35  Parda      3
##                      VD3005 VD4016
## 1 16 anos ou mais de estudo     NA
## 2         11 anos de estudo     NA
## 3         12 anos de estudo   1045
## 4          5 anos de estudo   1500
## 5          9 anos de estudo   1600
## 6         14 anos de estudo   3000

Um primeiro problema que me interessa resolver, é que os nomes de todas as variáveis da PNADC são códigos. Alguns pesquisadores experientes já decoraram esses códigos e conseguem trabalhar com elas. Mas como não sou um deles, prefiro mudar os nomes. Minimizo o R e vou consultar o dicionário da PNADC:

• V1022 = Situação do Domicílio
• V2007 = Sexo
• V2009 = Idade do morador
• V2010 = Raça/Cor
• VD2003 = Número de pessoas no domicílio
• VD3005 = Número de anos de estudo da pessoa
• VD4016 = Rendimento Mensal Habitual do Trabalho Principal

Então, decido que meu primeiro passo é alterar os nomes das variáveis no banco:

names(df) <- c("ano", "trimestre", "uf", "sit_dom", "sexo", "idade", "cor_pele", "n_moradores", "anos_estudo", "rend_mes_trab_princ")

head(df)

##    ano trimestre               uf sit_dom   sexo idade cor_pele n_moradores
## 1 2021         1            Ceará  Urbana  Homem    80   Branca           2
## 2 2021         1 Distrito Federal  Urbana Mulher    19    Parda           4
## 3 2021         1       Pernambuco  Urbana Mulher    36    Preta           2
## 4 2021         1   Santa Catarina  Urbana  Homem    50    Parda           2
## 5 2021         1        São Paulo  Urbana Mulher    43    Parda           3
## 6 2021         1            Goiás  Urbana  Homem    35    Parda           3
##                 anos_estudo rend_mes_trab_princ
## 1 16 anos ou mais de estudo                  NA
## 2         11 anos de estudo                  NA
## 3         12 anos de estudo                1045
## 4          5 anos de estudo                1500
## 5          9 anos de estudo                1600
## 6         14 anos de estudo                3000

Outra questão importante é se os tipos das variáveis estão corretos. Em geral, quero que meus números estejam registrados como numéricos, minhas categorias como fatores, etc.

str(df)

## 'data.frame':	1000 obs. of  10 variables:
##  $ ano                : int  2021 2021 2021 2021 2021 2021 2021 2021 2021 2021 ...
##  $ trimestre          : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ uf                 : chr  "Ceará" "Distrito Federal" "Pernambuco" "Santa Catarina" ...
##  $ sit_dom            : chr  "Urbana" "Urbana" "Urbana" "Urbana" ...
##  $ sexo               : chr  "Homem" "Mulher" "Mulher" "Homem" ...
##  $ idade              : int  80 19 36 50 43 35 72 23 23 47 ...
##  $ cor_pele           : chr  "Branca" "Parda" "Preta" "Parda" ...
##  $ n_moradores        : int  2 4 2 2 3 3 3 8 5 9 ...
##  $ anos_estudo        : chr  "16 anos ou mais de estudo" "11 anos de estudo" "12 anos de estudo" "5 anos de estudo" ...
##  $ rend_mes_trab_princ: int  NA NA 1045 1500 1600 3000 NA 1200 1200 2000 ...

Noto que minhas variáveis numéricas estão ok, mas minhas variáveis categóricas não. Elas estão registradas como “caractere”. Por isso, vou utilizar a coerção para transformá-las em fatores.

df$uf <- as.factor(df$uf)
df$sit_dom <- as.factor(df$sit_dom)
df$sexo <- as.factor(df$sexo)
df$cor_pele <- as.factor(df$cor_pele)
df$anos_estudo <- as.factor(df$anos_estudo)

Exercício

Uma outra opção é alterar um argumento durante a importação do meu banco, em read.csv. Que argumento é esse e como ele funcionaria aqui?

Voltando à aula, agora nosso banco tem a seguinte estrutura:

str(df)

## 'data.frame':	1000 obs. of  10 variables:
##  $ ano                : int  2021 2021 2021 2021 2021 2021 2021 2021 2021 2021 ...
##  $ trimestre          : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ uf                 : Factor w/ 27 levels "Acre","Alagoas",..: 6 7 17 24 25 9 3 25 7 10 ...
##  $ sit_dom            : Factor w/ 2 levels "Rural","Urbana": 2 2 2 2 2 2 2 2 2 1 ...
##  $ sexo               : Factor w/ 2 levels "Homem","Mulher": 1 2 2 1 2 1 1 2 1 1 ...
##  $ idade              : int  80 19 36 50 43 35 72 23 23 47 ...
##  $ cor_pele           : Factor w/ 5 levels "Amarela","Branca",..: 2 4 5 4 4 4 4 1 4 4 ...
##  $ n_moradores        : int  2 4 2 2 3 3 3 8 5 9 ...
##  $ anos_estudo        : Factor w/ 17 levels "1 ano de estudo",..: 8 3 4 12 16 6 8 4 6 12 ...
##  $ rend_mes_trab_princ: int  NA NA 1045 1500 1600 3000 NA 1200 1200 2000 ...

Uma primeira questão que me interessou explorar foram as estatísticas descritivas dos rendimentos do trabalho.

mean(df$rend_mes_trab_princ)

## [1] NA

Logo de cara, precisamos nos lembrar que a variável em questão tem valores nulos, então, é necessário utilizar argumentos nas funções de estatística.

mean(df$rend_mes_trab_princ, na.rm = TRUE)

## [1] 2000.636

median(df$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1262

range(df$rend_mes_trab_princ, na.rm = TRUE)

## [1]    50 19000

quantile(df$rend_mes_trab_princ, na.rm = TRUE)

##    0%   25%   50%   75%  100% 
##    50  1000  1262  2300 19000

sd(df$rend_mes_trab_princ, na.rm = TRUE)

## [1] 2128.755

Porém, uma questão me ocorreu: o rendimento mensal do trabalho é uma medida da capacidade das pessoas de atender suas necessidades, e os preços variam muito de cidade para cidade, de estado para estado, de região para região. Uma primeira providência que podemos tomar, é verificar as diferença entre a renda das populações urbana e rural.

df_urbana <- df[df$sit_dom == "Urbana", ]
df_rural <- df[df$sit_dom == "Rural", ]

mean(df_urbana$rend_mes_trab_princ, na.rm = TRUE)

## [1] 2236.528

median(df_urbana$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1500

range(df_urbana$rend_mes_trab_princ, na.rm = TRUE)

## [1]    50 19000

quantile(df_urbana$rend_mes_trab_princ, na.rm = TRUE)

##    0%   25%   50%   75%  100% 
##    50  1100  1500  2700 19000

sd(df_urbana$rend_mes_trab_princ, na.rm = TRUE)

## [1] 2313.148

mean(df_rural$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1199.136

median(df_rural$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1022.5

range(df_rural$rend_mes_trab_princ, na.rm = TRUE)

## [1]   50 5800

quantile(df_rural$rend_mes_trab_princ, na.rm = TRUE)

##     0%    25%    50%    75%   100% 
##   50.0  500.0 1022.5 1500.0 5800.0

sd(df_rural$rend_mes_trab_princ, na.rm = TRUE)

## [1] 968.0749

Podemos ver que os rendimentos da população urbana e rural são muito diferentes. A média e a mediana da renda urbana são de 1,5 a 2 vezes maior que a rural. Porém, eu posso conjecturar que a população rural teria um poder de compra maior, porque os preços dos produtos nas cidades são mais altos, e querer aplicar uma correção arbitrária de, digamos, 20%. Há diversas maneiras de levar isso a cabo, mas aqui, vou aproveitar para introduzir vocês a estrutura if else.

Vocês devem ter notado que eu usei 15 linhas de códigos para calcular as medidas de estatística descritiva, sendo que a maior parte dessas operações foi repetida três vezes com variação mínima linha por linha. A saída do R também não é muito útil, porque é difícil visualmente comparar grupos diferentes. Esse tipo de situação é perfeita para uma função.

descreva <- function(x) {
  mean(x, na.rm = TRUE)
  median(x, na.rm = TRUE)
  range(x, na.rm = TRUE)
  quantile(x, na.rm = TRUE)
  sd(x, na.rm = TRUE)
}

descreva(df$rend_mes_trab_princ)

## [1] 2128.755

Minha primeira tentativa de construir a função não deu muito certo. A função simplesmente retorna o primeiro valor. Isso faz parte do comportamento das funções em R, elas retornam apenas uma coisa. Mas eu tenho a solução: posso guardar todos os cálculos numa lista e a função a retornará.

descreva <- function(x) {
  
  list(
    Média         = mean(x, na.rm = TRUE),
    Mediana       = median(x, na.rm = TRUE),
    Amplitude     = range(x, na.rm = TRUE),
    Quartis       = quantile(x, na.rm = TRUE),
    Desvio_Padrão = sd(x, na.rm = TRUE)
  )
  
}

descreva(df$rend_mes_trab_princ)

## $Média
## [1] 2000.636
## 
## $Mediana
## [1] 1262
## 
## $Amplitude
## [1]    50 19000
## 
## $Quartis
##    0%   25%   50%   75%  100% 
##    50  1000  1262  2300 19000 
## 
## $Desvio_Padrão
## [1] 2128.755

Aproveitei também para melhorar minha função, nesse caso, optei simplesmente por colocar nomes nos elementos da lista. Agora posso facilmente descrever os meus três grupos:

# Renda total
descreva(df$rend_mes_trab_princ)

## $Média
## [1] 2000.636
## 
## $Mediana
## [1] 1262
## 
## $Amplitude
## [1]    50 19000
## 
## $Quartis
##    0%   25%   50%   75%  100% 
##    50  1000  1262  2300 19000 
## 
## $Desvio_Padrão
## [1] 2128.755

# Renda urbana
descreva(df_urbana$rend_mes_trab_princ)

## $Média
## [1] 2236.528
## 
## $Mediana
## [1] 1500
## 
## $Amplitude
## [1]    50 19000
## 
## $Quartis
##    0%   25%   50%   75%  100% 
##    50  1100  1500  2700 19000 
## 
## $Desvio_Padrão
## [1] 2313.148

# Renda rural
descreva(df_rural$rend_mes_trab_princ)

## $Média
## [1] 1199.136
## 
## $Mediana
## [1] 1022.5
## 
## $Amplitude
## [1]   50 5800
## 
## $Quartis
##     0%    25%    50%    75%   100% 
##   50.0  500.0 1022.5 1500.0 5800.0 
## 
## $Desvio_Padrão
## [1] 968.0749

Até aqui, tudo bem, mas e a minha correção?

if

Para aplicar essa correção, decidi inflar a renda rural em 20% e diminuir a renda urbana em 10%. Não sei se esses valores fazem sentido, mas vamos partir do pressuposto que sim. Como eu poderia colocar isso dentro da minha função descreva de tal forma que o resultado reflita a minha correção? Preciso de uma estrutura que execute uma operação para rendas urbanas e outra para rendas rurais. Algo assim:

teste1 <- data.frame(renda = 2000,
                    sit_dom = "rural")
teste1

##   renda sit_dom
## 1  2000   rural

teste2 <- data.frame(renda = 2000,
                    sit_dom = "urbana")
teste2

##   renda sit_dom
## 1  2000  urbana

if (teste1$sit_dom[1] == "urbana") {
  mean(teste1$renda[1] * 0.9)
}

if (teste1$sit_dom[1] == "rural") {
  mean(teste1$renda[1] * 1.2)
}

## [1] 2400

if (teste2$sit_dom[1] == "urbana") {
  mean(teste2$renda[1] * 0.9)
}

## [1] 1800

if (teste2$sit_dom[1] == "rural") {
  mean(teste2$renda[1] * 1.2)
}

Ok, isso resolve meu problema de uma forma muito simples:

• A estrutura if realiza um teste lógico dentro dos parênteses que deve retornar um valor único
• Se este valor for TRUE, a operação dentro dos {} será realizada.

Vocês podem testar alterar os valores de “teste” e verificar se o resultado muda.

Porém, esse tipo de estrutura tem duas limitações importantes:

• Só funciona para testes lógicos que retornam um único valor TRUE/FALSE
• Exige que o computador execute um teste lógico para cada operação, mesmo que ele já tenha encontrado o caso verdadeiro

A solução para o primeiro problema a gente vê mais tarde, mas a solução para o segundo é você criar uma árvore de decisão para seu problema, indicando o que fazer em cada caso.

else

No caso mais simples, só temos duas alternativas, então se/senão.

teste <- data.frame(renda = 2000,
                    sit_dom = "rural")
teste

##   renda sit_dom
## 1  2000   rural

if (teste$sit_dom[1] == "urbana") {
  mean(teste$renda[1] * 0.9)
} else {
  mean(teste$renda[1] * 1.2)
}

## [1] 2400

Experimentem alterar os valores de teste para ver o resultado.

Tudo bem, mas como eu posso utilizar isso na prática? Eu preciso calcular as minhas estatísticas descritivas, e esse caso é muito simples. Podemos levá-lo para dentro da nossa função descreva. Vamos criar uma outra função parecida:

descreva2 <- function(x, y) {
  # Se todos os valores de y forem urbana
  if (all(y == "Urbana")) {
    # altere os valores de x
    x <- x * 0.9
    # e calcule as estatísticas descritivas
    list(
      Média         = mean(x, na.rm = TRUE),
      Mediana       = median(x, na.rm = TRUE),
      Amplitude     = range(x, na.rm = TRUE),
      Quartis       = quantile(x, na.rm = TRUE),
      Desvio_Padrão = sd(x, na.rm = TRUE)
    )
  # senão, a população é rural
  } else {
    # altere os valores de x
    x <- x * 1.2
    # e calcule as estatísticas descritivas
    list(
      Média         = mean(x, na.rm = TRUE),
      Mediana       = median(x, na.rm = TRUE),
      Amplitude     = range(x, na.rm = TRUE),
      Quartis       = quantile(x, na.rm = TRUE),
      Desvio_Padrão = sd(x, na.rm = TRUE)
    )
  }
  
}

descreva2(df_urbana$rend_mes_trab_princ, df_urbana$sit_dom)

## $Média
## [1] 2012.876
## 
## $Mediana
## [1] 1350
## 
## $Amplitude
## [1]    45 17100
## 
## $Quartis
##    0%   25%   50%   75%  100% 
##    45   990  1350  2430 17100 
## 
## $Desvio_Padrão
## [1] 2081.833

descreva2(df_rural$rend_mes_trab_princ, df_rural$sit_dom)

## $Média
## [1] 1438.964
## 
## $Mediana
## [1] 1227
## 
## $Amplitude
## [1]   60 6960
## 
## $Quartis
##   0%  25%  50%  75% 100% 
##   60  600 1227 1800 6960 
## 
## $Desvio_Padrão
## [1] 1161.69

descreva2 agora aplica a minha correção, mas ela ainda tem diversos problemas. Ela não sabe como lidar com meu banco de dados completo, que contém tanto casos urbanos, como rurais. Mas para nossos propósitos, ela serve. Isso nos traz para uma lição muito importante: todo código é uma obra incompleta, ele pode ser melhorado e tornado mais genérico e poderoso, mas será que vale a pena?

Como analistas, precisamos valorizar o nosso tempo: cada dia que passamos programando e refinando nossos códigos, é um dia que poderia ser gasto com leituras, comunicação, escrita, etc. Em geral, minha regra de ouro é o good enough. Se o seu código realiza corretamente as operações que são do seu interesse naquele momento no tempo, ele é bom. Você deve melhorá-lo apenas se surgir um novo caso em que ele não corresponde mais às suas necessidades.

Lookup tables

Continuamos nossa análise e me ocorreu outra questão, as diferenças nos rendimentos de pessoas de acordo com a sua cor da pele. Eu poderia começar calculando as medidas de tendência central para cada grupo:

branca <- df[df$cor_pele == "Branca", ]
preta <- df[df$cor_pele == "Preta", ]
parda <- df[df$cor_pele == "Parda", ]
amarela <- df[df$cor_pele == "Amarela", ]
indigena <- df[df$cor_pele == "Indígena", ]

mean(branca$rend_mes_trab_princ, na.rm = TRUE)

## [1] 2391.827

mean(preta$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1722.571

mean(parda$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1679.492

mean(amarela$rend_mes_trab_princ, na.rm = TRUE)

## [1] 2300

mean(indigena$rend_mes_trab_princ, na.rm = TRUE)

## [1] NaN

median(branca$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1500

median(preta$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1100

median(parda$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1100

median(amarela$rend_mes_trab_princ, na.rm = TRUE)

## [1] 1700

median(indigena$rend_mes_trab_princ, na.rm = TRUE)

## [1] NA

Bastante coisa pra digitar né? Mais tarde vamos ver uma solução para este problema. Mas no momento, estou interessado em uma questão mais específica: por causa do pequeno número de observações, e também por causa de considerações metodológicas, eu quero reduzir o número de categorias de cor da pele para três: Branca, Negra e Outra. Eu poderia utilizar estruturas de if/else, mas a implementação seria um pouco longa:

cor1 <- "Branca"

cor2 <- "Parda"

cor3 <- "Indígena"

mude_corpele <- function(x) {
  if (x == "Branca") {
    x
  } else if (x == "Preta") {
    "Negra"
  } else if (x == "Parda") {
    "Negra"
  } else {
    "Outra"
  }
}

mude_corpele(cor1)

## [1] "Branca"

mude_corpele(cor2)

## [1] "Negra"

mude_corpele(cor3)

## [1] "Outra"

Eu também precisaria de um jeito de repetir essa operação muitas vezes, talvez com um laço, que veremos adiante. Mas nesse tipo de caso específico, há uma saída muito mais elegante, rápida e fácil: lookup tables. Conceitualmente, lookup tables são como uma tabelinha no qual você diz ao computador para procurar um resultado que corresponde a uma chave. Por exemplo:

• Branca -> Branca
• Preta -> Negra
• Parda -> Negra
• Amarela -> Outra
• Indígena -> Outra

E aí, o computador vai repetir a operação de “olhar” a tabela para ver a qual valor corresponde qual chave a quantidade de vezes que for necessário. Veja como a implementação fica simples:

mudecor <-c(Branca   = "Branca",
            Preta    = "Negra",
            Parda    = "Negra",
            Amarela  = "Outra",
            Indígena = "Outra")

Agora, eu posso obter o valor correspondente fazer usando indexação:

mudecor["Branca"]

##   Branca 
## "Branca"

mudecor["Preta"]

##   Preta 
## "Negra"

mudecor["Parda"]

##   Parda 
## "Negra"

mudecor["Amarela"]

## Amarela 
## "Outra"

mudecor["Indígena"]

## Indígena 
##  "Outra"

E é fácil fazer o mesmo para todas as observações salvas no vetor df$cor_pele, desde que façamos um passo intermediário de coerção para “caractere”.

mudecor[as.character(df$cor_pele)]

##   Branca    Parda    Preta    Parda    Parda    Parda    Parda  Amarela 
## "Branca"  "Negra"  "Negra"  "Negra"  "Negra"  "Negra"  "Negra"  "Outra" 
##    Parda    Parda   Branca    Parda    Parda    Parda    Parda    Parda 
##  "Negra"  "Negra" "Branca"  "Negra"  "Negra"  "Negra"  "Negra"  "Negra" 
##    Parda    Preta    Preta    Parda    Parda   Branca   Branca    Parda 
##  "Negra"  "Negra"  "Negra"  "Negra"  "Negra" "Branca" "Branca"  "Negra" 
##    Parda    Parda    Preta   Branca    Parda   Branca    Parda   Branca 
##  "Negra"  "Negra"  "Negra" "Branca"  "Negra" "Branca"  "Negra" "Branca" 
##    Parda    Parda   Branca   Branca   Branca   Branca   Branca   Branca 
##  "Negra"  "Negra" "Branca" "Branca" "Branca" "Branca" "Branca" "Branca" 
....
Saída truncada para visualização

Para salvar esse resultado no data frame, ficaríamos com:

df$cor_pele2 <- mudecor[as.character(df$cor_pele)]

head(df [ sample(1:nrow(df), 5), c("cor_pele", "cor_pele2") ] )

##     cor_pele cor_pele2
## 490    Parda     Negra
## 841    Parda     Negra
## 136    Parda     Negra
## 553   Branca    Branca
## 326    Parda     Negra

Note que eu optei por salvar o resultado numa nova variável, chamada cor_pele2. Em geral, essa é a abordagem correta, você preserva a sua variável original e cria uma variável derivada dela, mas existem situações em que pode ser mais adequado alterar a variável original. Cabe a vocês refletir sobre o “preço” que se paga por esta opção no caso concreto de vocês.

Utilizando uma lookup table, pulamos o problema de ter que repetir a operação uma vez para cada observação, nos aproveitando do comportamento do R quando utilizamos a indexação de data frames com [].

Comentários

Aproveito que mudamos a função descreva para falar sobre o uso de comentários # no código. São informações que o computador ignora ao rodar o programa, mas cuja presença ajuda o leitor a rapidamente compreender o que um determinado código faz sem precisar mergulhar nos detalhes. Comentários são cruciais para que o programa seja legível para outras pessoas, como seus colaboradores e para seu “eu futuro”, que pode voltar àquele programa original muito tempo depois e ter dificuldade de compreender o que ele está fazendo. Volte para a função descreva e a função descreva2 e veja a diferença entre as duas.

Comentários fazem parte da documentação de códigos, e um bom uso deles ajuda você a aprender programação, manter códigos, colaborar com outras pessoas e identificar problemas rapidamente. Criem o hábito de escreverem comentários nos seus programas.

No começo, é comum a gente escrever muitos comentários, detalhando todas as tarefas. Com o tempo, os nossos códigos vão ficando mais enxutos, e deixamos a própria linguagem fazer a maior parte da comunicação, com alguns comentários aqui e ali apenas para situar o leitor.

Isso é relevante porque nossos códigos são documentos textuais, como mensagens, memorandos e relatórios. Eles se assemelham muito a uma seção “Métodos” de um artigo científico, porque descrevem as tarefas realizadas para chegar a um resultado. Portanto, boas práticas de produção de textos como pontuação, estilo, conectores, coesão e coerência são importantes aqui também. Esse é um assunto discutido na “Programação Literária” e foge um pouco do tema desse curso.

Loops

Voltando para o nosso banco de dados, agora que recategorizamos a variável renda, temos que resolver um segundo problema: preciso calcular a média e a mediana da renda para cada grupo da variável cor_pele2. Já vimos que podemos fazer isso com muita digitação lá em cima, mas não é difícil imaginar situações em que o número de grupos é muito grande e isso não seja recomendado. Além disso, códigos que exigem muita digitação são cansativos e nos levam a cometer muitos erros.

Por essas razões, a solução mais adequada é utilizar laços:

# Primeiro, separamos os grupos
grupos <- unique(df$cor_pele2)
grupos

## [1] "Branca" "Negra"  "Outra"

# Iniciamos um vetor que armazenará nossos resultados
renda_corpele2 <- vector(length = 3L)

# Aqui começa o laço
for (i in 1:3) {
  renda_corpele2[i] <- mean(df$rend_mes_trab_princ[df$cor_pele2 == grupos[i]], na.rm = TRUE)
}

# E aqui está o resultado
renda_corpele2

## [1] 2391.827 1686.537 2300.000

for

O laço acima tem diversos passos, e é muito instrutivo se a gente olhar para cada um deles com cuidado.

• A primeira parte, no qual separamos os grupos, não uma parte do laço em si, mas ela é necessária nesse contexto em que vamos fazer operações por grupo.
• A segunda parte é a inicialização de um espaço vazio para conter nossos resultados. Ao contrário da maioria das funções que vimos até o momento, for loops não retornam nada. Experimente rodar um for loop em que você não atribui <- os resultados a nenhum objeto. Nesse caso, queremos um espaço para cada grupo, então um vetor vazio de tamanho 3.
• A terceira parte é a sequência, que vai nos parênteses e indica qual o nome do operador sequencial, no caso, eu o chamei de i, e os valores que i vai tomar em cada repetição, no caso, 1, 2 e 3.
• A quarta parte, é o corpo, onde as operações são de fato executadas. Em geral, o corpo de um loop só contém uma operação mesmo, mas isso não é obrigatório! Um for loop pode conter diversas operações dentro de seu corpo. O único cuidado é que todo resultado deve ser atribuído <- a algum objeto, ou ele será perdido.
• Por fim, é praxe imprimir o resultado após a execução para verificação.

Veja também este segundo loop:

sexos <- unique(df$sexo)

rend_medio_sexo <- vector(length = 2L)
rend_mediano_sexo <- vector(length = 2L)

for (i in 1:2) {
  rend_medio_sexo[i] <- mean(df$rend_mes_trab_princ[df$sexo == sexos[i]], na.rm = TRUE)
  rend_mediano_sexo[i] <- median(df$rend_mes_trab_princ[df$sexo == sexos[i]], na.rm = TRUE)
}

rend_medio_sexo

## [1] 2121.893 1817.175

rend_mediano_sexo

## [1] 1308 1200

Espero que tenha ficado claro pra vocês que com um pouco mais de trabalho vocês conseguem rapidamente calcular todas as medidas de estatística descritiva por grupos incrementando esse tipo de estrutura de laço com mais vetores e mais operações.

Outros loops

Existem também outras estruturas de loops em R, como o while e o repeat. Optamos por não incluir elas no curso porque elas acabam não sendo muito relevantes para a análise de dados em R. Os alunos interessados em aprender mais sobre elas podem consultar os manuais de referência do curso, os livros Hands-on Programming with R e Ciência de dados em R descrevem brevemente como essas estruturas funcionam.

O resumão é que o loop while funciona através de um teste lógico: o laço é repetido enquanto o teste lógico retornar verdadeiro e você é responsável por programar dentro do corpo as mudanças entre uma repetição e outra que eventualmente levarão o teste a falhar. O repeat loop é parecido, mas a diferença é que ele será repetido indefinidamente e você é responsável por introduzir a condição que o fará parar com break.

Vetorização

Esse assunto é opcional, talvez não interesse tanta gente. Voltemos para a situação em que queremos transformar a variável cor_pele. Ao invés da solução que encontramos utilizando lookup tables, poderíamos muito bem criar uma árvore de decisão if/else dentro de um for loop.

# Inicialização
df$cor_pele3 <- NA

# Sequência e corpo
for (i in 1:nrow(df)) {
  if (df$cor_pele[i] == "Branca") {
    df$cor_pele3[i] <- "Branca"
  } else if (df$cor_pele[i] == "Preta") {
    df$cor_pele3[i] <- "Negra"
  } else if (df$cor_pele[i] == "Parda") {
    df$cor_pele3[i] <- "Negra"
  } else {
    df$cor_pele3[i] <- "Outra"
  }
}

# Resultado
df[1:10, c("cor_pele", "cor_pele2", "cor_pele3")]

##    cor_pele cor_pele2 cor_pele3
## 1    Branca    Branca    Branca
## 2     Parda     Negra     Negra
## 3     Preta     Negra     Negra
## 4     Parda     Negra     Negra
## 5     Parda     Negra     Negra
## 6     Parda     Negra     Negra
## 7     Parda     Negra     Negra
## 8   Amarela     Outra     Outra
## 9     Parda     Negra     Negra
## 10    Parda     Negra     Negra

O resultado é o mesmo. Porém, algumas perguntas pra vocês:

• Qual das duas soluções envolve mais digitação (e chance de cometer erros)?
• Qual das duas soluções roda mais rápido em um banco de dados grande?
• Qual das duas soluções é mais legível para uma pessoa olhando de fora?

Algumas dessas perguntas tem respostas subjetivas, mas uma delas, a performance, tem uma resposta objetiva:

system.time({
  df$cor_pele2 <- mudecor[as.character(df$cor_pele)]
})

##   usuário   sistema decorrido 
##         0         0         0

system.time({
  df$cor_pele3 <- NA
  for (i in 1:nrow(df)) {
    if (df$cor_pele[i] == "Branca") {
      df$cor_pele3[i] <- "Branca"
    } else if (df$cor_pele[i] == "Preta") {
      df$cor_pele3[i] <- "Negra"
    } else if (df$cor_pele[i] == "Parda") {
      df$cor_pele3[i] <- "Negra"
    } else {
      df$cor_pele3[i] <- "Outra"
    }
  }
})

##   usuário   sistema decorrido 
##      0.05      0.00      0.05

Vejam que mesmo em um banco de dados pequeno, com apenas mil observações, a operação vetorizada foi quase instantânea, enquanto o for loop demorou alguns milisegundos. Na hora que passamos para operações com milhares ou milhões de observações, essa diferença se traduz em tempo perdido e vale a pena considerar procurar uma solução vetorizada para o nosso problema.

O outro ponto que acho importante levantar é que existe uma correspondência entre esses dois tipos de estrutura: sempre que você vir um código que faz uma árvore de decisão dentro de um for loop, provavelmente é um problema que pode ser facilmente resolvido com uma lookup table. De quebra, você ainda tem um código muito mais rápido.

Infelizmente, por uma questão de tempo e foco, vamos deixar de fora a ideia de programação funcional, no qual a gente transforma nossos laços em funções e utiliza a família de funções apply do R para repetir a aplicação de funções para a maioria dos casos em que utilizaríamos for loops. Mas fica como uma sugestão de estudo pros alunos que se pegarem usando muitos for loops. Também não falamos de ambientes, funções genéricas e métodos no sistema S3, que ficam como leituras recomendadas nos livros de referência.

Em termos de conteúdo, o curso se encerra por aqui, ficamos agora com a revisão e os exercícios.

Revisão

Programas são uma sequência lógica de operações em série e em paralelo que nos levam de uma coleção de entradas (em geral, bancos de dados) para as nossas saídas desejadas (em geral, estatísticas e gráficos, outros bancos de dados transformados, etc.).

É uma boa ideia separar o seu programa da sua implementação e sempre ter à mão o seu programa a medida que você trabalha para colocá-lo em prática na sua linguagem de programação favorita (que é, obviamente, o R). Você pode executar partes do seu programa dentro e fora do R, dependendo das suas necessidades.

Seus passos em série são implementados apenas ordenando suas operações de cima para baixo, enquanto seus passos em paralelo dependem do uso de estruturas lógicas se-então-senão e de laços.

Uma solução para alguns tipos de operação é o uso de lookup tables, elas tem a vantagem de serem simples em sua estrutura e rodarem muito rapidamente.

O laço mais comum no cinto de utilidades do analista é o for, ele é composto de uma inicialização, uma sequência e um corpo. Sua principal qualidade é a flexibilidade, já que ele pode ser utilizado para repetir qualquer tipo de operação um determinado número de vezes. Existem outros tipos de laço, mas eles não são tão importantes para nós.

A vetorização de operações é uma forma de ganhar velocidade nos códigos. O uso de lookup tables é um exemplo de vetorização de árvores if-else e for loops, mas vale considerar que soluções vetorizadas podem ser mais trabalhosas de desenvolver do que laços. Então sempre tenha em mente que seu tempo é precioso e um código good enough te permite usá-lo para outras tarefas mais relevantes.

Exercícios

1. Amanhã teremos nossa oficina livre, em que vocês devem desenvolver seu primeiro programa de forma autônoma, embora com a nossa presença e apoio. Comece desenvolvendo um bloco de notas (físico ou virtual) o passo a passo das operações que você deveria realizar. Uma boa maneira de representar códigos é utilizar fluxogramas, que representar esquematicamente a estrutura das operações, a presença de atividades em série, em paralelo e laços.

2. Qual o valor de x no código abaixo:

x <- 1
if (x == 1) {
  x <- x + 1
  if (x == 1) {
    x <- x + 1
  }
}
x

3. E no código abaixo?

x <- 1
if (x == 1) {
  x <- x + 1
  if (x == 2) {
    x <- x + 1
  }
}
x

## [1] 3

4. O que o código abaixo está fazendo? Como você utilizaria esse código? Você consegue pensar em outra solução para o mesmo problema?

x <- c(1, 2, 3)

if (x == 1) {
  "empregado"
} else if (x == 2) {
  "desempregado"
} else {
  "desalentado"
}

## Warning in if (x == 1) {: a condição tem comprimento > 1 e somente o primeiro
## elemento será usado

## [1] "empregado"

5. Construa um loop que calcule a idade média de cada uf.

6. Construa um código que calcule a média do número de moradores do domicílio, segundo situação urbana ou rural. O que os resultados te dizem?

7. Construa duas maneiras de calcular o rendimento anual do trabalho principal,

• uma operação simples com vetores
• utilizando um for loop